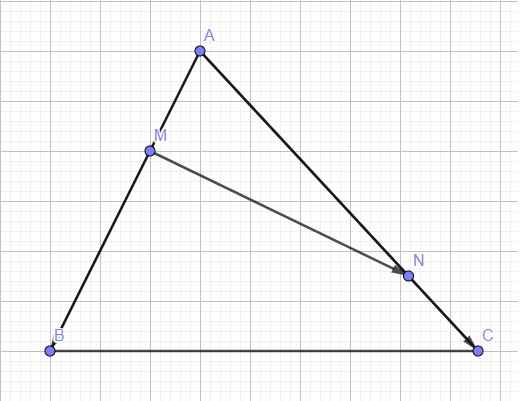
\(BM=2AM\Rightarrow BM=\dfrac{2}{3}AB\Rightarrow\overrightarrow{MB}=\dfrac{2}{3}\overrightarrow{AB}\)
\(AN=3CN\Rightarrow CN=\dfrac{1}{4}CA\Rightarrow\overrightarrow{CN}=\dfrac{1}{4}\overrightarrow{CA}\)
Ta có:
\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{BC}+\dfrac{1}{4}\overrightarrow{CA}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{BC}+\dfrac{1}{4}\left(\overrightarrow{CB}+\overrightarrow{BA}\right)\)
\(=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{BC}+\dfrac{1}{4}\overrightarrow{CB}+\dfrac{1}{4}\overrightarrow{BA}=\dfrac{2}{3}\overrightarrow{AB}+\overrightarrow{BC}-\dfrac{1}{4}\overrightarrow{BC}-\dfrac{1}{4}\overrightarrow{AB}\)
\(=\dfrac{5}{12}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{BC}\)
Lời giải:
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\frac{1}{3}\overrightarrow{BA}+\frac{3}{4}\overrightarrow{AC}\)
\(=\frac{-1}{3}\overrightarrow{AB}+\frac{3}{4}(\overrightarrow{AB}+\overrightarrow{BC})=\frac{5}{12}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{BC}\)