Bài 1: Rút gọn biểu thức: 3) √50+2√8-√2 + √125 6)(3√2-√5)-15-12 c) 5v40-3v25a + √9a Bài 2: giải phương trình: 7/2√8x-√18x-9-√2x Bai 3: Cho hàm số y=-1/2x có đồ thị (d) và hàm số y = 2x-5 có đồ thị (d'). a) Về (d) và (d') trên cùng một hệ trục tọa độ b) Tìm tọa độ giao điểm của (d) và (d') bằng phép tính. c) tính góc tạo bởi đường thẳng (d') và trục Ox Bài 5: Cho tam giác ABC vuông tại A có AB >AC. Đường tròn tâm O đường kính AB cắt BC tại D. a/Chứng minh: AC²=CD.CB b) Đường vuông góc với OC kẻ từ A cắt OC tại F và cắt đường tròn tâm O tại E (E khác A) Chứng minh: CE là tiếp tuyến của (O)
Bài 5:
a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)DB tại D
=>AD\(\perp\)BC tại D
Xét ΔABC vuông tại A có AD là đường cao
nên \(AC^2=CD\cdot CB\)
b: Ta có: ΔOAE cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOE
Xét ΔOAC và ΔOEC có
OA=OE
\(\widehat{AOC}=\widehat{EOC}\)
OC chung
Do đó: ΔOAC=ΔOEC
=>\(\widehat{OAC}=\widehat{OEC}\)
mà \(\widehat{OAC}=90^0\)
nên \(\widehat{OEC}=90^0\)
=>CE là tiếp tuyến của (O)
Bài 3:
a: 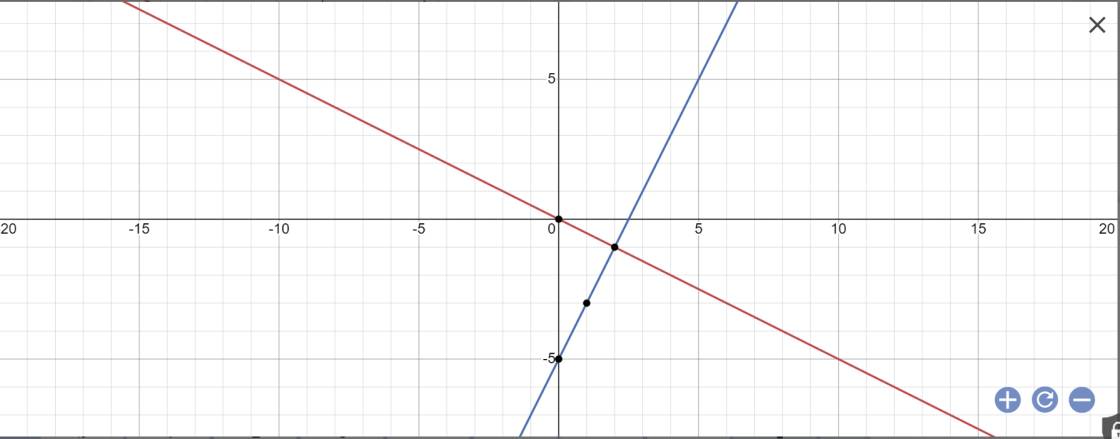
b: Phương trình hoành độ giao điểm là:
\(-\dfrac{1}{2}x=2x-5\)
=>\(-\dfrac{1}{2}x-2x=-5\)
=>\(-\dfrac{5}{2}x=-5\)
=>x=2
Thay x=2 vào y=-1/2x, ta được:
\(y=-\dfrac{1}{2}\cdot2=-1\)
Vậy: (d) cắt (d') tại điểm A(2;-1)












