Để bài toán thỏa mãn thì \(m\le\max\limits_{\left[-1;1\right]}g\left(x\right)\) với \(g\left(x\right)=f\left(-f\left(x\right)\right)\)
\(g'\left(x\right)=-f'\left(x\right).f'\left(-f\left(x\right)\right)\)
Trên \(\left[-1;1\right]\) ta thấy \(f\left(x\right)\) nghịch biến nên \(-f'\left(x\right)\ge0\) ; \(\forall x\)
\(\Rightarrow\) Dấu và cực trị của \(g\left(x\right)\) phụ thuộc vào \(f'\left(-f\left(x\right)\right)\)
\(f'\left(-f\left(x\right)\right)=0\Rightarrow\left[{}\begin{matrix}-f\left(x\right)=-1\\-f\left(x\right)=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}f\left(x\right)=-1\\f\left(x\right)=1\end{matrix}\right.\) (1)
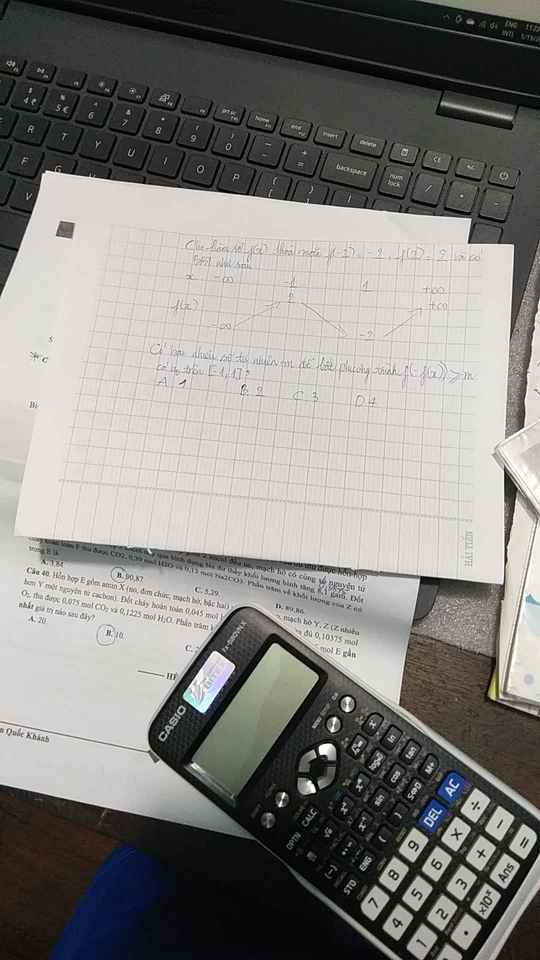
Từ BBT ta thấy trên \(\left[-1;1\right]\) thì \(f\left(x\right)=-1\) và \(f\left(x\right)=1\) có 2 nghiệm pb \(a\) và \(b\) (mỗi pt 1 nghiệm) sao cho \(-1< b< a< 1\)
(Nhớ rằng a và b lần lượt là nghiệm của (1) nên \(\left\{{}\begin{matrix}f\left(a\right)=-1\\f\left(b\right)=1\end{matrix}\right.\))
Do đó để tìm max \(g\left(x\right)\) trên \(\left[-1;1\right]\) thì chỉ cần tính toán giá trị tại các đầu mút và điểm dừng:
\(g\left(-1\right)=f\left(-f\left(-1\right)\right)=f\left(-2\right)=-2\);
\(g\left(1\right)=f\left(-f\left(1\right)\right)=f\left(2\right)=2\)
\(g\left(a\right)=f\left(-f\left(a\right)\right)=f\left(-\left(-1\right)\right)=f\left(1\right)=-2\) ;
\(g\left(b\right)=f\left(-f\left(b\right)\right)=f\left(-1\right)=2\)
\(\Rightarrow g\left(x\right)_{max}=2\Rightarrow m\le2\Rightarrow\) có 3 số tự nhiên thỏa mãn
//Nếu trắc nghiệm, nhìn đồ thị có thể dễ dàng nghịch suy ra hàm \(f\left(x\right)=x^3-3x\) như sau:
Dạng đồ thị \(f\left(x\right)\) có dạng bậc 3, có 2 cực trị \(x=\pm1\) do đó \(f'\left(x\right)=a\left(x-1\right)\left(x+1\right)=a\left(x^2-1\right)\)
Nguyên hàm lên ta được: \(f\left(x\right)=a\left(\dfrac{x^3}{3}-x\right)+C\)
Thay \(\Rightarrow\left\{{}\begin{matrix}x=1\Rightarrow f\left(x\right)=-2\\x=-1\Rightarrow f\left(x\right)=2\end{matrix}\right.\) được hệ: \(\left\{{}\begin{matrix}-\dfrac{2}{3}a+C=-2\\\dfrac{2}{3}a+C=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}C=0\\a=3\end{matrix}\right.\)
Tới đây suy ra \(f\left(x\right)=x^3-3x\Rightarrow g\left(x\right)=\left(3x-x^3\right)^3-\left(3x-x^3\right)\)
Đưa vào mode 7 table nhập hàm rồi dò max trên \(\left[-1;1\right]\) là ra m luôn