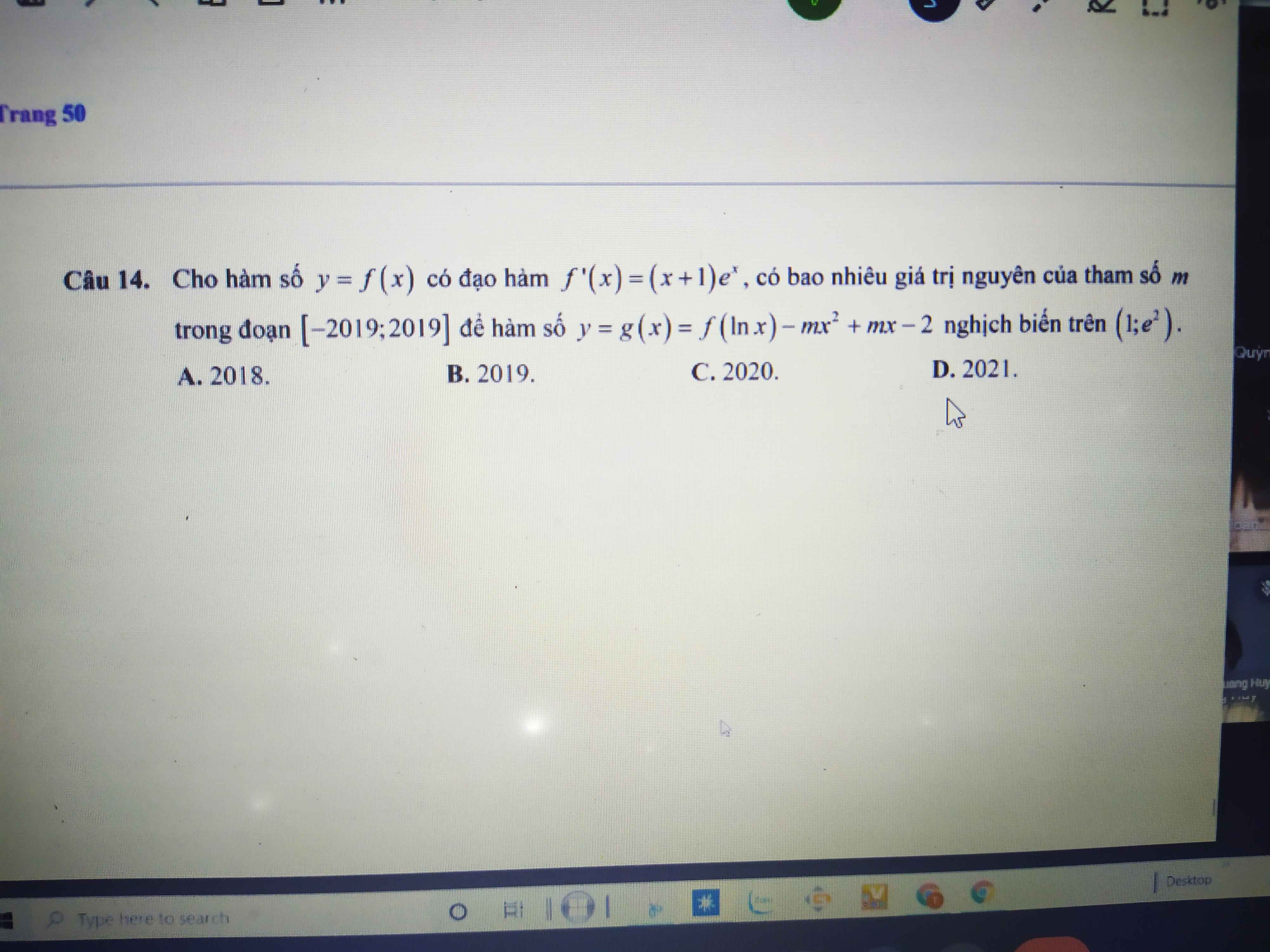
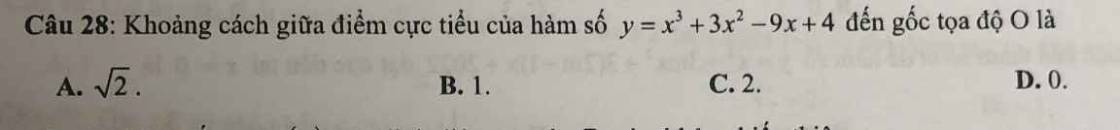\(y=x^3+3x^2-9x+4\)
=>\(y'=3x^2+3\cdot2x-9=3x^2+6x-9\)
=>\(y''=3\cdot2x+6=6x+6\)
Đặt y'=0
=>\(3x^2+6x-9=0\)
=>\(x^2+2x-3=0\)
=>(x+3)(x-1)=0
=>\(\left[{}\begin{matrix}x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=1\end{matrix}\right.\)
Khi x=-3 thì \(y''=6\cdot\left(-3\right)+6=-18+6=-12< 0\)
=>x=-3 là cực đại của hàm số
Khi x=1 thì \(y''=6\cdot1+6=12>0\)
=>x=1 là cực tiểu của hàm số
Khi x=1 thì \(y=1^3+3\cdot1^2-9\cdot1+4=-1\)
=>A(1;-1) là cực tiểu của hàm số
\(AO=\sqrt{1^2+1^2}=\sqrt{2}\)
=>Chọn A