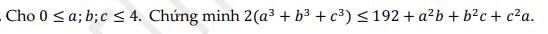Ta có :
\(0\le a;b;c\le4\)
\(\Leftrightarrow\left(16-a^2\right)\left(4-b\right)\ge0\)
\(\Leftrightarrow64-16b-4a^2+a^2b\ge0\)
\(\Leftrightarrow64+a^2b\ge16b+4a^2\)
\(\Leftrightarrow64+a^2b\ge4\left(a^2+4b\right)\ge a^3+b^3\left(1\right)\)
Chứng minh tương tự :
\(\left\{{}\begin{matrix}64+b^2c\ge b^3+c^3\left(2\right)\\64+c^2a\ge c^3+a^3\left(3\right)\end{matrix}\right.\)
\(\left(1\right)+\left(2\right)+\left(3\right)\)
\(\Leftrightarrow2\left(a^3+b^3+c^3\right)\le192+a^2b+b^2c+c^2a\)
\(\Rightarrow dpcm\)
Đúng 1
Bình luận (0)
