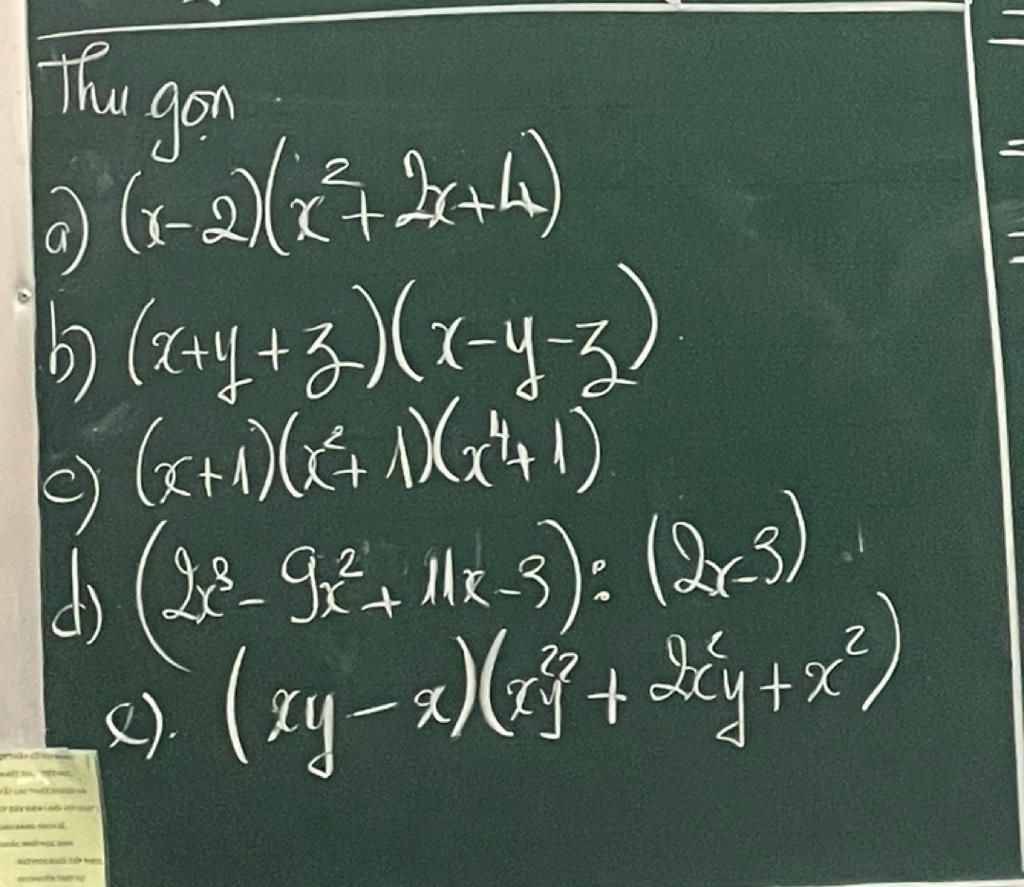a) \(\left(x-2\right)\left(x^2+2x+4\right)\)
\(=\left(x-2\right)\left(x^2+2\cdot x+2^2\right)\)
\(=x^3-2^3\)
\(=x^3-8\)
b) \(\left(x+y+3\right)\left(x-y-3\right)\)
\(=x^2-xy-3x+xy-y^2-3y+3x-3y-9\)
\(=x^2-y^2-6y-9\)
c) \(\left(x+1\right)\left(x^2+1\right)\left(x^4+1\right)\)
\(=\left(x^3+x+x^2+1\right)\left(x^4+1\right)\)
\(=x^7+x^3+x^5+x+x^6+x^2+x^4+1\)
\(=x^7+x^6+x^5+x^4+x^3+x^2+x+1\)
d) \(\left(2x^3-9x^2+11x-3\right):\left(2x-3\right)\)
\(=\left(2x^3-6x^2+2x-3x^2+9x-3\right):\left(2x-3\right)\)
\(=\left[2x\left(x^2-3x+1\right)-3\left(x^2+3x-1\right)\right]:\left(2x-3\right)\)
\(=\left(2x-3\right)\left(x^2-3x+1\right):\left(2x-3\right)\)
\(=x^2-3x+1\)
e) \(\left(xy-x\right)\left(x^2y^2+2x^2y+x^2\right)\)
\(=\left(xy-x\right)\left[\left(xy\right)^2-2xy\cdot x+x^2\right]\)
\(=\left(xy\right)^3-x^3\)
\(=x^3y^3-x^3\)
a) ( x − 2 ) ( x 2 + 2 x + 4 ) = ( x − 2 ) ( x 2 + 2 ⋅ x + 2 2 ) = x 3 − 2 3 = x 3 − 8 b) ( x + y + 3 ) ( x − y − 3 ) = x 2 − x y − 3 x + x y − y 2 − 3 y + 3 x − 3 y − 9 = x 2 − y 2 − 6 y − 9 c) ( x + 1 ) ( x 2 + 1 ) ( x 4 + 1 ) = ( x 3 + x + x 2 + 1 ) ( x 4 + 1 ) = x 7 + x 3 + x 5 + x + x 6 + x 2 + x 4 + 1 = x 7 + x 6 + x 5 + x 4 + x 3 + x 2 + x + 1 d) ( 2 x 3 − 9 x 2 + 11 x − 3 ) : ( 2 x − 3 ) = ( 2 x 3 − 6 x 2 + 2 x − 3 x 2 + 9 x − 3 ) : ( 2 x − 3 ) = [ 2 x ( x 2 − 3 x + 1 ) − 3 ( x 2 + 3 x − 1 ) ] : ( 2 x − 3 ) = ( 2 x − 3 ) ( x 2 − 3 x + 1 ) : ( 2 x − 3 ) = x 2 − 3 x + 1 e) ( x y − x ) ( x 2 y 2 + 2 x 2 y + x 2 ) = ( x y − x ) [ ( x y ) 2 − 2 x y ⋅ x + x 2 ] = ( x y ) 3 − x 3 = x 3 y 3 − x 3