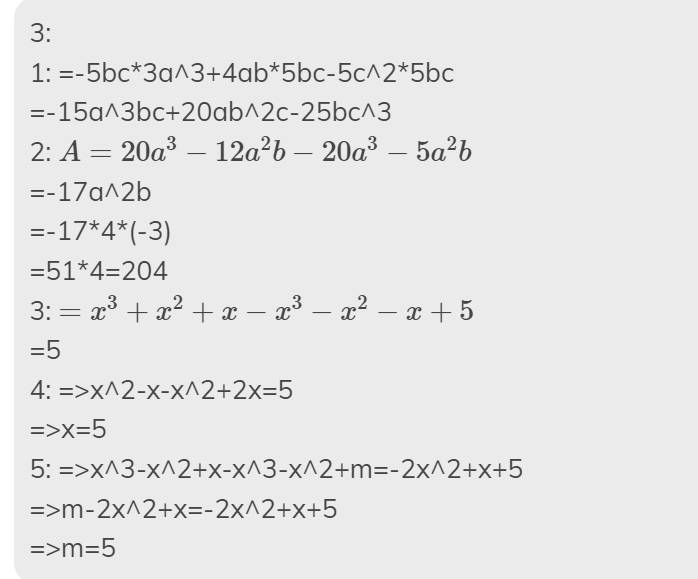Bài 3:
1) \(\left(3a^3-4ab+5c^2\right)\left(-5bc\right)\)
\(=\left(3a^3\cdot-5bc\right)+\left(-4ab\cdot-5bc\right)+\left(5c^2\cdot-5bc\right)\)
\(=-15a^3bc+20ab^2c-25bc^3\)
2) \(A=4a^2\left(5a-3b\right)-5a^2\left(4a+b\right)\)
\(A=20a^3-12a^2b-20a^3-5a^2b\)
\(A=-19a^2b\)
Thay a=-2, b=-3 vào A ta có:
\(-19\cdot\left(-2\right)^2\cdot\left(-3\right)=228\)
3) \(B=x\left(x^2+x+1\right)-x^2\left(x+1\right)-x+5\)
\(B=x^3+x^2+x-x^3-x^2-x+5\)
\(=5\)
Vậy giá trị của biểu thức không phụ thuộc vào biến
4) \(x\left(x-1\right)-x^2+2x=5\)
\(\Leftrightarrow x^2-x-x^2+2x=5\)
\(\Leftrightarrow x=5\)
5) \(\left(x^2-x+1\right)x-\left(x+1\right)x^2+m=-2x^2+x+5\)
\(\Leftrightarrow x^3-x^2+x-x^3-x^2+m=-2x^2+x+5\)
\(\Leftrightarrow-2x^2+x+m=-2x^2+x+5\)
\(\Leftrightarrow-2x^2+2x^2+x-x+m=5\)
\(\Leftrightarrow m=5\)