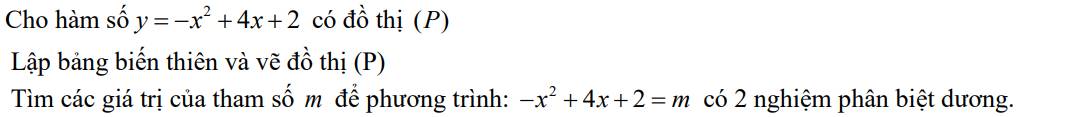Question

Answer 1

a: Tọa độ đỉnh là:

\(\left\{{}\begin{matrix}x=\dfrac{-4}{2\cdot\left(-1\right)}=\dfrac{4}{2}=2\\y=-\dfrac{4^2-4\cdot\left(-1\right)\cdot2}{4\cdot\left(-1\right)}=6\end{matrix}\right.\)

Bảng biến thiên:

x	-∞                2                            +
y	-∞                6                          -∞

b: -x^2+4x+2=m

=>-x^2+4x+2-m=0

=>x^2-4x+m-2=0

\(\Delta=\left(-4\right)^2-4\left(m-2\right)=16-4m+8=-4m+24\)

Để phương trình có hai nghiệm phân biệt dương thì

\(\left\{{}\begin{matrix}-4m+24>0\\\dfrac{4}{1}>0\\\dfrac{m-2}{1}>0\end{matrix}\right.\Leftrightarrow2< m< 6\)