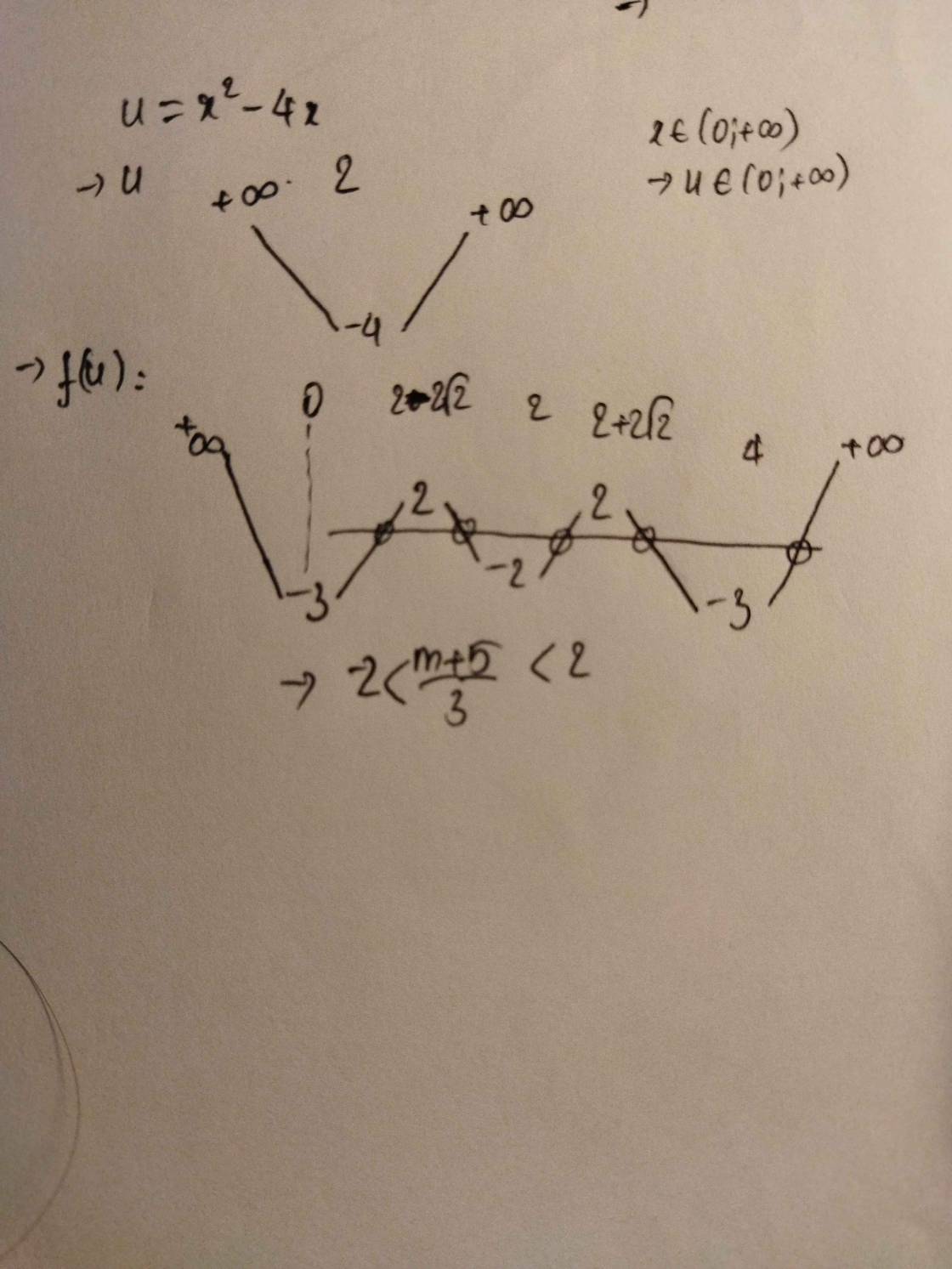
Đặt \(g\left(x\right)=x^2-4x=t\) (1) với \(x>0\)
\(g'\left(x\right)=4x-4=0\Rightarrow x=1\)
\(f\left(0\right)=0\) ; \(f\left(1\right)=-4\)
\(\Rightarrow\) \(-4< t< 0\) thì (1) có 2 nghiệm x, \(\left[{}\begin{matrix}t=-4\\t\ge0\end{matrix}\right.\) thì (1) có 1 nghiệm x
Pt đã cho trở thành \(3f\left(t\right)=m+5\Rightarrow f\left(t\right)=\dfrac{m+5}{3}\) (2)
Từ BBT ta thấy để pt đã cho có 5 nghiệm:
TH1: (2) có 1 nghiệm t thuộc (-4;0) và 3 nghiệm thỏa mãn \(\left[{}\begin{matrix}t=-4\\t\ge0\end{matrix}\right.\) (không thỏa mãn)
TH2: (2) có 2 nghiệm thuộc (-4;0) và 1 nghiệm thỏa \(\left[{}\begin{matrix}t=-4\\t\ge0\end{matrix}\right.\)
\(\Rightarrow-2< \dfrac{m+5}{3}< 2\Rightarrow-11< m< 1\)
\(\Rightarrow\) Có 11 giá trị nguyên của m thỏa mãn