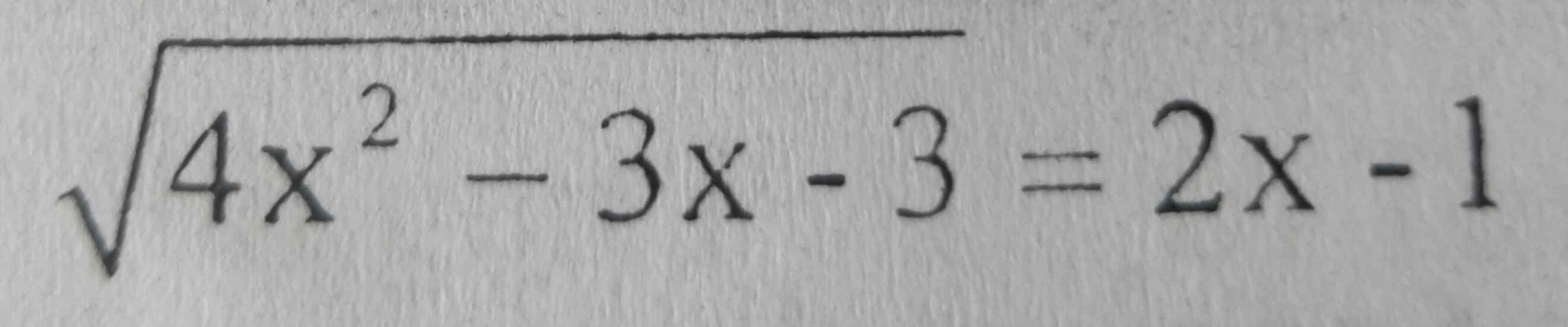Question

Answer 1

\(\Leftrightarrow\left\{{}\begin{matrix}x>=\dfrac{1}{2}\\4x^2-3x-3=4x^2-4x+1\end{matrix}\right.\Leftrightarrow x=4\)

Answer 2

`sqrt{4x^2-3x-3} = 2x-1`

`Đk : 2x-1 >=0 <=> x >=1/2`

`<=> 4x^2 -3x -3 = (2x-1)^2`

`<=> 4x^2 -3x-3 = 4x^2 - 4x+1`

`<=> 4x^2 -3x-4x^2 +4x = 1+3`

`<=> x = 4 (t//m)`

Vậy `S={4}`