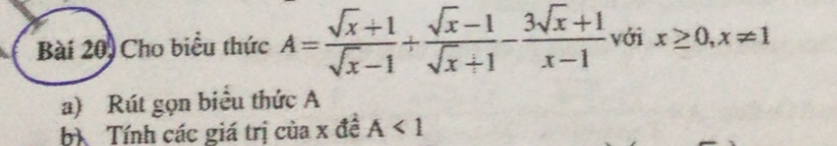`a)` Với `x >= 0,x \ne 1` có:
`A=[\sqrt{x}+1]/[\sqrt{x}-1]+[\sqrt{x}-1]/[\sqrt{x}+1]-[3\sqrt{x}+1]/[x-1]`
`A=[(\sqrt{x}+1)^2+(\sqrt{x}-1)^2-3\sqrt{x}-1]/[(\sqrt{x}-1)(\sqrt{x}+1)]`
`A=[x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1]/[(\sqrt{x}-1)(\sqrt{x}+1)]`
`A=[2x-3\sqrt{x}+1]/[(\sqrt{x}-1)(\sqrt{x}+1)]`
`A=[(2\sqrt{x}-1)(\sqrt{x}-1)]/[(\sqrt{x}-1)(\sqrt{x}+1)]`
`A=[2\sqrt{x}-1]/[\sqrt{x}+1]`
__________________________________________________________
`b)` Với `x >= 0,x \ne 1` có:
`A < 1<=>[2\sqrt{x}-1]/[\sqrt{x}+1] < 1`
`<=>[2\sqrt{x}-1-\sqrt{x}-1]/[\sqrt{x}+1] < 0`
Mà với `x >= 0,x \ne 1<=>\sqrt{x}+1 > 0`
`=>\sqrt{x}-2 < 0<=>\sqrt{x} < 2<=>x < 4`
Kết hợp đk
`=>0 <= x < 4,x \ne 1`
\(a,A=\dfrac{\left(\sqrt{x}+1\right)^2+\left(\sqrt{x}-1\right)^2-3\sqrt{x}-1}{x-1}\\ =\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{x-1}\\ =\dfrac{2x-3\sqrt{x}+1}{x-1}\\ =\dfrac{2x-2\sqrt{x}-\sqrt{x}+1}{x-1}\\ =\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)}{x-1}\\ =\dfrac{\left(2\sqrt{x}-1\right)\left(\sqrt{x}-1\right)}{x-1}\\ =\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
\(\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}< 1\\ \dfrac{2\sqrt{x}-1-\sqrt{x}-1}{\sqrt{x}+1}< 0\\ \sqrt{x}-2< 0\\ \sqrt{x}< 2\\ x< 4\)
KH vs đk xđ
\(0\le x< 4;x\ne1\)