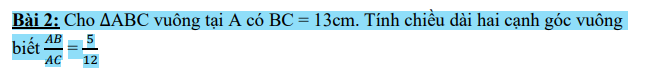Question

Answer 1

Đặt AB/5=AC/12=k

=>AB=5k; AC=12k

Xét ΔABC vuông tại A có \(AB^2+AC^2=BC^2\)

\(\Leftrightarrow25k^2+144k^2=169\)

\(\Leftrightarrow169k^2=169\)

=>k=1

=>AB=5cm; AC=12cm

Answer 2

`[AB]/[AC]=5/12=>AB=5/12AC`

Xét `\triangle ABC` vuông tại `A` có:

    `AB^2+AC^2=BC^2`

`=>(5/12AC)^2+AC^2=13^2`

`=>169/144AC^2=169`

`=>AC^2=144`

`=>AC=12(cm)`

 Mà `AB=5/12AC`

   `=>AB=5/12 .12=5(cm)`