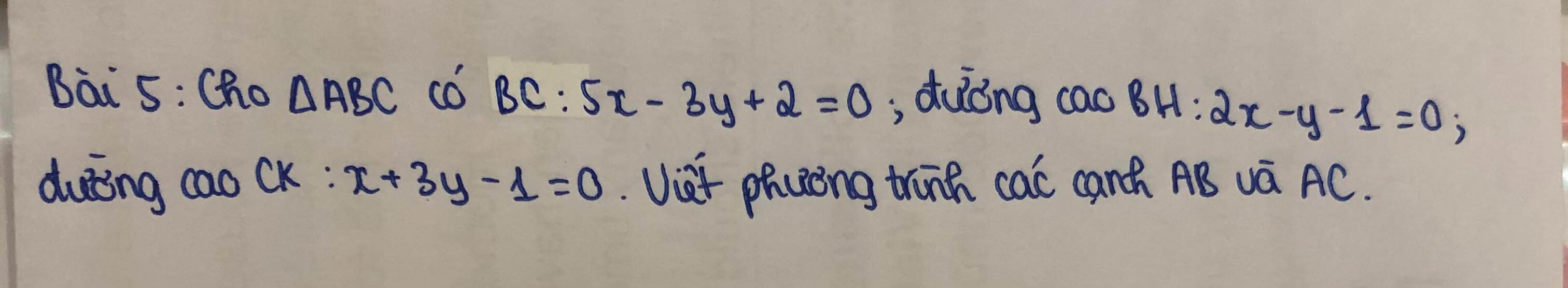B là giao điểm BC và BH nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}5x-3y+2=0\\2x-y-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=9\end{matrix}\right.\) \(\Rightarrow B\left(5;9\right)\)
Đường thẳng AB vuông góc CK nên nhận (3;-1) là 1 vtpt
Phương trình AB:
\(3\left(x-5\right)-1\left(y-9\right)=0\Leftrightarrow3x-y-6=0\)
C là giao điểm BC và CK nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}5x-3y+2=0\\x+3y-1=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{6}\\y=\dfrac{7}{18}\end{matrix}\right.\) \(\Rightarrow C\left(-\dfrac{1}{6};\dfrac{7}{18}\right)\)
Đường thẳng AC vuông góc BH nên nhận (1;2) là 1 vtpt
Phương trình AC:
\(1\left(x+\dfrac{1}{6}\right)+2\left(y-\dfrac{7}{18}\right)=0\Leftrightarrow...\)