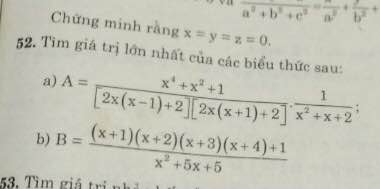\(A=\dfrac{x^4+x^2+1}{\left(2x^2+2\right)^2-4x^2}.\dfrac{1}{x^2+x+2}=\dfrac{x^4+x^2+1}{4\left(x^4+x^2+1\right)}.\dfrac{1}{x^2+x+2}\)
\(=\dfrac{1}{4x^2+4x+8}=\dfrac{1}{\left(2x+1\right)^2+7}\le\dfrac{1}{7}\)
\(A_{max}=\dfrac{1}{7}\) khi \(x=-\dfrac{1}{2}\)
\(B=\dfrac{\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)+1}{x^2+5x+5}=\dfrac{\left(x^2+5x+4\right)\left(x^2+5x+6\right)+1}{x^2+5x+5}\)
\(=\dfrac{\left(x^2+5x+5-1\right)\left(x^2+5x+5+1\right)+1}{x^2+5x+5}=\dfrac{\left(x^2+5x+5\right)^2-1+1}{x^2+5x+5}\)
\(=x^2+5x+5\)
Biểu thức B chỉ có min, không tồn tại max (đề bài sai)
Đúng 0
Bình luận (0)
