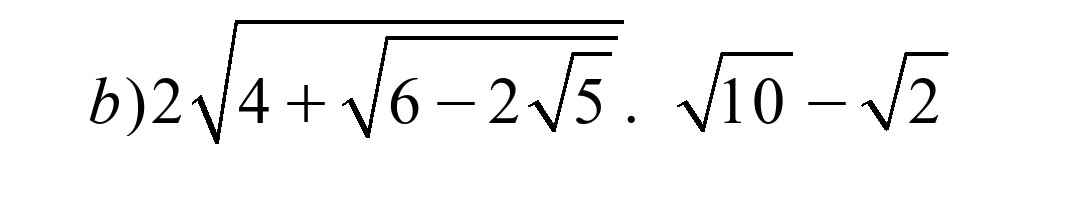\(2\sqrt{4+\sqrt{6-2\sqrt{5}}}.\sqrt{10}-\sqrt{2}\)
\(=2\sqrt{4+\sqrt{\left(\sqrt{5}-1\right)^2}}.\sqrt{10}-\sqrt{2}\)
\(=2\sqrt{3+\sqrt{5}}.\sqrt{10}-\sqrt{2}\)
\(=2\sqrt{6+2\sqrt{5}}.\sqrt{5}-\sqrt{2}\)
\(=2\sqrt{\left(\sqrt{5}+1\right)^2}.\sqrt{5}-\sqrt{2}\)
\(=2\left(\sqrt{5}+1\right).\sqrt{5}-\sqrt{2}\)
\(=10+2\sqrt{5}-\sqrt{2}\)
Ta có: \(2\cdot\sqrt{4+\sqrt{6-2\sqrt{5}}}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=2\cdot\sqrt{4+\sqrt{5}-1}\cdot\left(\sqrt{10}-\sqrt{2}\right)\)
\(=\sqrt{2}\cdot\sqrt{6-2\sqrt{5}}\cdot\sqrt{2}\cdot\left(\sqrt{5}-1\right)\)
\(=2\left(6-2\sqrt{5}\right)\)
\(=12-4\sqrt{5}\)