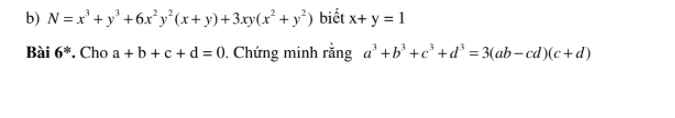6/ Ta có:
\(a+b=-c-d\)
\(\Leftrightarrow\left(a+b\right)^3=-\left(c+d\right)^3\)
\(\Leftrightarrow a^3+3ab^2+3a^{2b}+b^3=c^3+3c^2d+3cd^2+d^3\)
\(\Leftrightarrow a^3+b^3+c^3+d^3=-3\left(a^2b+ab^2+c^2d+cd^2\right)\)
\(\Leftrightarrow a^3+b^3+c^3+d^3=-3\left[ab\left(a+b\right)+cd\left(c+d\right)\right]\)
\(\Leftrightarrow a^3+b^3+c^3+d^3=-3\left[-ab\left(c+d\right)+cd\left(c+d\right)\right]\)
\(\Leftrightarrow a^3+b^3+c^3+d^3=-3\left(c+d\right)\left(cd-ab\right)\)
\(\Leftrightarrow a^3+b^3+c^3+d^3=3\left(c+d\right)\left(ab-cd\right)\)
b/
\(N=x^3+y^3+6x^2y^2\left(x+y\right)+3xy\left(x^2+y^2\right)\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+6x^2y^2+3xy\left(\left(x+y\right)^2-2xy\right)\)
\(=\left(\left(x+y\right)^2-3xy\right)+6x^2y^2+3xy\left(1-2xy\right)\)
\(=\left(1-3xy\right)+6x^2y^2+3xy\left(1-2xy\right)=1\)