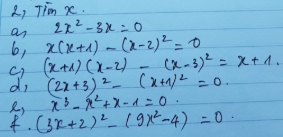Mik ra đáp án là
a) Th1:x=3
Th2:x=2
b) Th1:x=0
Th2:x=5/2
c) x=2
a) \(\left(2x-1\right)^2-25=0\)
\(\Leftrightarrow\left(2x-1\right)^5=25\)
\(\Leftrightarrow2x-1=5\)
\(\Leftrightarrow x=3\)
b) \(8x^3-50x=0\)
\(\Leftrightarrow2x\left(4x^2-25\right)=0\)
\(\Leftrightarrow2x\left(x^2-\dfrac{25}{4}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-\dfrac{25}{4}=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\pm\dfrac{5}{2}\end{matrix}\right.\)
c) \(\left(x-2\right)\left(x^2+2x+7\right)+2\left(x^2-4\right)-5\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+2x+7+2x+4-5\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x^2+4x+6\right)=0\) (*)
mà \(x^2+4x+6=\left(x+2\right)^2+2\ge2\forall x\)
(*) \(\Rightarrow x-2=0\Rightarrow x=2\)

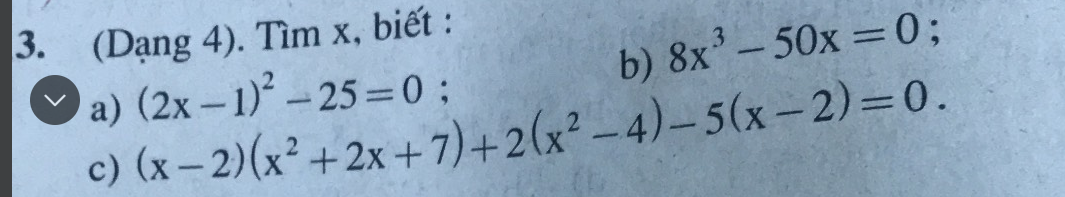












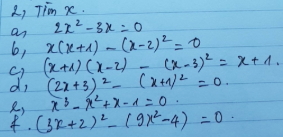 Không làm tắt
Không làm tắt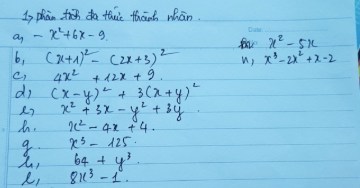 Ko làm tắt
Ko làm tắt