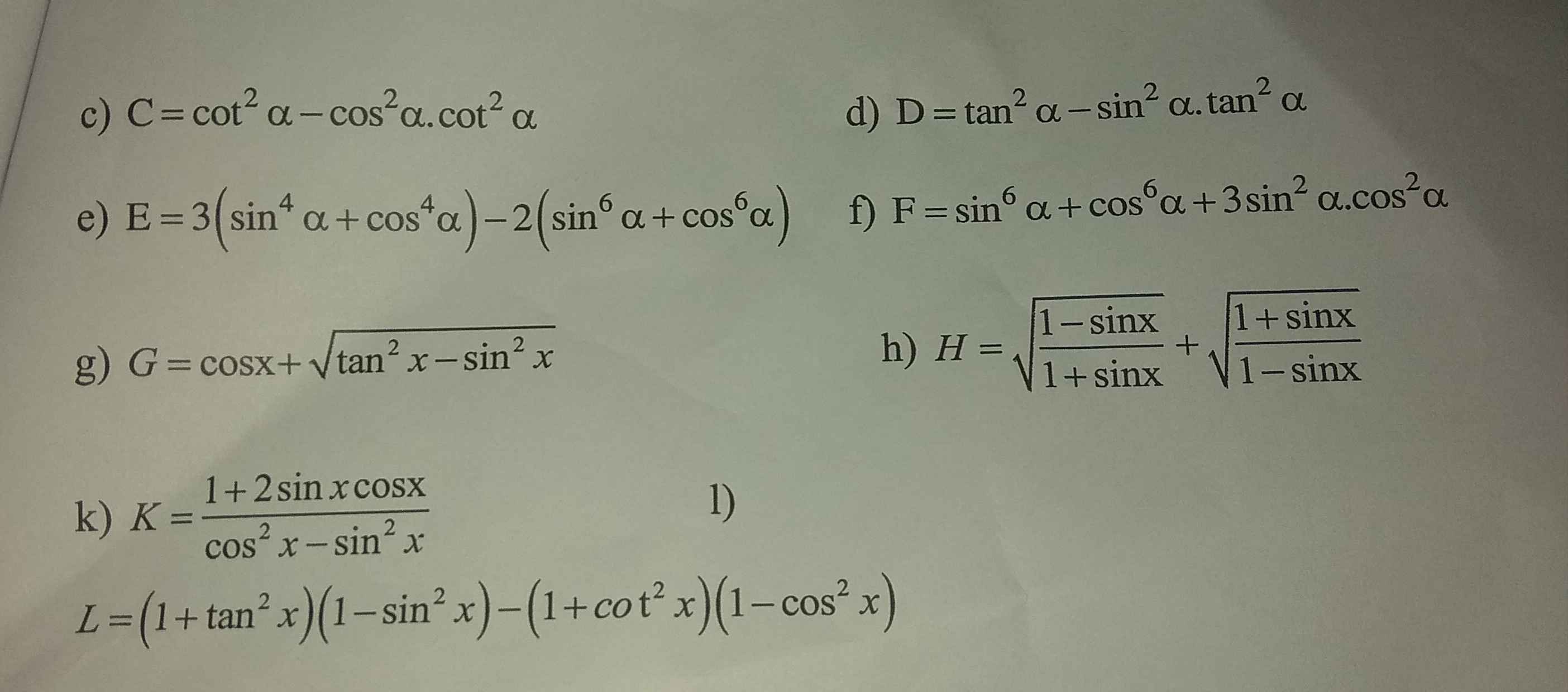1.
\(sin^2a+cos^2a=1\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{4}{5}\)
\(tana=\dfrac{sina}{cosa}=\dfrac{3}{4}\)
\(cota=\dfrac{1}{tana}=\dfrac{4}{3}\)
2.
\(A=sin^2a+cos^2a+2sina.cosa+sin^2a+cos^2a-2sina.cosa\)
\(=2\left(sin^2a+cos^2a\right)=2.1=2\)
\(B=sina.cosa\left(\dfrac{sina}{cosa}+\dfrac{cosa}{sina}\right)=sina.cosa\left(\dfrac{sin^2a+cos^2a}{sina.cosa}\right)\)
\(=sin^2a+cos^2a=1\)
\(C=cot^2a\left(1-cos^2a\right)=\dfrac{cos^2a}{sin^2a}.sin^2a=cos^2a\)
\(D=tan^2a.\left(1-sin^2a\right)=\dfrac{sin^2a}{cos^2a}.cos^2a=sin^2a\)
\(E=3\left[\left(sin^2a+cos^2a\right)-2sin^2a.cos^2a\right]-2\left[\left(sin^2a+cos^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)\right]\)
\(=3\left(1-2sin^2a.cos^2a\right)-2\left(1-3sin^2a.cos^2a\right)\)
\(=3-6sin^2a.cos^2a-2+6sin^2a.cos^2a\)
\(=1\)
\(F=\left(sin^2a+cos^2a\right)^3-3sin^2a.cos^2a\left(sin^2a+cos^2a\right)+3sin^2a.cos^2a\)
\(=1-3sin^2a.cos^2a+3sin^2a.cos^2a\)
\(=1\)
\(G=cosx+\sqrt{\dfrac{sin^2x}{cos^2x}-sin^2x}=cosx+\sqrt{sin^2x\left(\dfrac{1}{cos^2x}-1\right)}\)
\(=cosx+sinx\sqrt{\dfrac{1-cos^2x}{cos^2x}}\)
\(=cosx+sinx\sqrt{\dfrac{sin^2x}{cos^2x}}\)
\(=cosx+\dfrac{sin^2x}{cosx}=\dfrac{cos^2x+sin^2x}{cosx}\)
\(=\dfrac{1}{cosx}\)
\(H=\dfrac{\left(1-sinx\right)+\left(1+sinx\right)}{\sqrt{\left(1+sinx\right)\left(1-sinx\right)}}=\dfrac{2}{\sqrt{1-sin^2x}}=\dfrac{2}{\sqrt{cos^2x}}=\dfrac{2}{cosx}\)
\(K=\dfrac{sin^2x+cos^2x+2sinx.cosx}{cos^2x-sin^2x}=\dfrac{\left(cosx+sinx\right)^2}{\left(cosx-sinx\right)\left(cosx+sinx\right)}\)
\(=\dfrac{cosx+sinx}{cosx-sinx}\)
\(L=\left(1+\dfrac{sin^2x}{cos^2x}\right).cos^2x-\left(1+\dfrac{cos^2x}{sin^2x}\right).sin^2x\)
\(=\dfrac{\left(cos^2x+sin^2x\right)cos^2x}{cos^2x}-\dfrac{\left(sin^2x+cos^2x\right).sin^2x}{sin^2x}\)
\(=cos^2x+sin^2x-\left(sin^2x+cos^2x\right)\)
\(=0\)
Bài 1:
\(\cos\alpha=\sqrt{1-\sin^2\alpha}=\sqrt{1-\dfrac{9}{25}}=\dfrac{4}{5}\)
\(\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{3}{5}:\dfrac{4}{5}=\dfrac{3}{4}\)
\(\cot\alpha=\dfrac{\cos\alpha}{\sin\alpha}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)