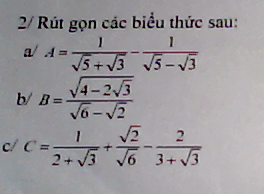Lời giải:
a.
\(A=\frac{\sqrt{5}-\sqrt{3}-(\sqrt{5}+\sqrt{3})}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}=\frac{-2\sqrt{3}}{5-3}=-\sqrt{3}\)
b.
\(B=\frac{\sqrt{(\sqrt{3}-1)^2}}{\sqrt{2}(\sqrt{3}-1)}=\frac{|\sqrt{3}-1|}{\sqrt{2}(\sqrt{3}-1)}=\frac{\sqrt{3}-1}{\sqrt{2}(\sqrt{3}-1)}=\frac{1}{\sqrt{2}}\)
c.
\(C=\frac{2-\sqrt{3}}{(2-\sqrt{3})(2+\sqrt{3})}+\frac{\sqrt{12}}{6}-\frac{2(3-\sqrt{3})}{(3-\sqrt{3})(3+\sqrt{3})}\)
\(=\frac{2-\sqrt{3}}{2^2-3}+\frac{2\sqrt{3}}{6}-\frac{2(3-\sqrt{3})}{3^2-3}\)
\(=2-\sqrt{3}+\frac{\sqrt{3}}{3}-(1-\frac{\sqrt{3}}{3})=\frac{3-\sqrt{3}}{3}\)
b) Ta có: \(B=\dfrac{\sqrt{4-2\sqrt{3}}}{\sqrt{6}-\sqrt{2}}\)
\(=\dfrac{\sqrt{3}-1}{\sqrt{2}\left(\sqrt{3}-1\right)}\)
\(=\dfrac{\sqrt{2}}{2}\)
c) Ta có: \(C=\dfrac{1}{2+\sqrt{3}}+\dfrac{\sqrt{2}}{\sqrt{6}}-\dfrac{2}{3+\sqrt{3}}\)
\(=\dfrac{12-6\sqrt{3}}{6}+\dfrac{\sqrt{12}}{6}-\dfrac{2\left(3-\sqrt{3}\right)}{6}\)
\(=\dfrac{12-6\sqrt{3}+2\sqrt{3}-6+2\sqrt{3}}{6}\)
\(=\dfrac{6-2\sqrt{3}}{6}\)
\(=\dfrac{3-\sqrt{3}}{3}\)