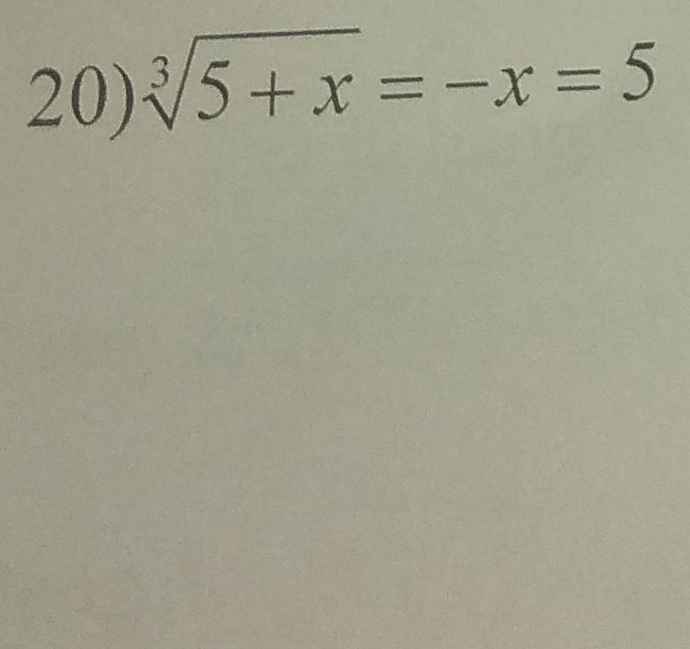20) Ta có: \(\sqrt[3]{5+x}=-x=5\)
\(\Leftrightarrow\left\{{}\begin{matrix}5+x=\left(-x\right)^3\\5+x=125\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=100\\5+100=\left(-100\right)^3\left(loại\right)\end{matrix}\right.\)
Vậy: \(S=\varnothing\)
\(\sqrt[3]{5+x}-x=5\\ \Leftrightarrow\sqrt[3]{5+x}=x+5\\ \Leftrightarrow\sqrt[3]{5+x}\left(\sqrt[3]{\left(5+x\right)2}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt[3]{5+x}=0\\\sqrt[3]{\left(5+x\right)^2=1}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-4\\x=-6\end{matrix}\right.\)