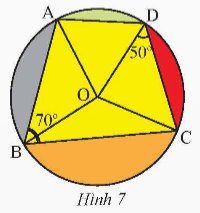
Trong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Cho biết \(\widehat {ABC}\) = 70o, \(\widehat {OCD}\) = 50o. Tìm góc \(\widehat {AOD}\).
Cho \(\Delta ABC\) có ba góc nhọn nội tiếp đường tròn (O;R), AD là đường cao của \(\Delta ABC\) và AM là đường kính của đường tròn tâm O, gọi E là hình chiếu của B trên AM.
a) CM: \(\widehat{ACM}=90^o\) và \(\widehat{BAD}=\widehat{MAC}\)
b) CM: Tứ giác ABDE nội tiếp
c) CM: DE//BC
a: góc ACM=1/2*sđ cung AM=90 độ
góc BAD+góc ABD=90 độ
góc MAC+góc AMC=90 độ
mà góc ABD=góc AMC
nên góc BAD=góc MAC
b: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
Cho hình chữ nhật ABCD nội tiếp đường tròn tâm O. Trên cung nhỏ AB lấy điểm E ( E ko trùng A và B), F là giao của AB và CE.
a) CM tứ giác FBHE nội tiếp
b) CM \(\widehat{FHA}=\widehat{ADE}\) ???
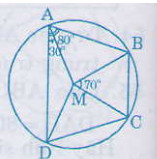
Cho ABCD là một tứ giác nội tiếp đường tròn tâm M, biết \(\widehat{DAB}=80^o,\widehat{DAM}=30^o;\widehat{BMC}=70^o.\)
Hãy tính số đo các góc \(\widehat{MAB};\widehat{BCM};\widehat{AMB};\widehat{DMC};\widehat{AMD};\widehat{MCD}\) và \(\widehat{BCD}.\)
Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD

Ta có: =
-
= 80o – 30o = 50o (1)
- ∆MBC là tam giác cân (MB= MC) nên =
= 55o (2)
- ∆MAB là tam giác cân (MA=MB) nên = 50o (theo (1))
Vậy = 180o – 2. 50o = 80o
=
sđcung BCD (số đo góc nội tiếp bằng nửa số đo của cung bị chắn)
=> sđ cung BCD = 2 = 2. 80o = 160o
Mà sđ cung BC = = 70o (số đo ở tâm bằng số đo cung bị chắn)
Vậy cung DC = 160o – 70o = 90o (vì C nằm trên cung nhỏ cung BD)
Suy ra = 90o (4)
∆MAD là tam giác cân (MA= MD)
Suy ra = 180o – 2.30o = 120o (5)
∆MCD là tam giác vuông cân (MC= MD) và = 90o
Suy ra =
= 45o (6)
= 100o theo (2) và (6) và vì CM là tia nằm giữa hai tia CB, CD
cho tứ giác ABCD nội tiếp đường tròn tâm O. biết phân giác trong của \(\widehat{BAD}\) và \(\widehat{ABC}\) cắt nhau tại E trên cạnh CD.
1. CM: AD+BC=CD
2. cho \(\dfrac{CD}{CB}=k\) (k>1). tính tỉ số diện tích ΔADE và ΔBCE
Cho đường tròn tâm $O$, đường kính $AD = 2R$. Vẽ dây cung tâm $D$ bán kính $R$, cung này cắt đường tròn $(O)$ ở $B$ và $C$.
a) Tứ giác $OBDC$ là hình gì? Vì sao?
b) Tính số đo các góc \(\widehat{CBD};\widehat{CBO};\widehat{OBA}\)
c) Chứng minh tam giác $ABC$ là tam giác đều.
cho đường tròn tâm O , từ A ở ngoài đường tròn vẽ 2 tiếp tuyến AB, AC với đường tròn tâm O . kẻ dây CD//AB . Nối AD cắt đường tròn tâm O tại E. C/M:
a/ tứ giác ABOC nội tiếp
b/ AB2 = AE.AD
c/ \(\widehat{AOC}\)= \(\widehat{ACB}\) và tam giác BCD cân
2/ Cho tam giác ABC có các đường cao BD và CE , đường thẳng DE cắt đường tròn ngoại tiếp tam giác ABC tại M và N . C/m :
a. tứ giác BEDC nội tiếp
b. \(\widehat{DEA}\) = \(\widehat{ACB}\)
C.DE // tiếp tuyến tại A của đường tròn ngoại tiếp tam giác ABC
a) Xét (O) có :
AB là tiếp tuyến tại B
AC là tiếp tuyến tại C
AB cắt AC tại A
\(\Rightarrow\widehat{ABO}=\widehat{ACO}=90^o\)và OA là p/g \(\widehat{BOC}\)
Xét tg ABOC có \(\widehat{ABO}+\widehat{ACO}=180^o\)Mà 2 góc này đối nhau
\(\Rightarrow\)ABOC là tg nt
b) Xét (O) có
\(\widehat{ABE}\)là góc tạo bởi tiếp tuyến AB và dây BE
\(\widehat{BDE}\)là góc nt chắn cung BE
\(\Rightarrow\widehat{ABE}=\widehat{BDE}=\frac{1}{2}sđ\widebat{BE}\)
Xét \(\Delta ABEvà\Delta ADB:\)
\(\widehat{BAD}\)chung
\(\widehat{ABE}=\widehat{BDE}\)
\(\Rightarrow\Delta ABE\infty\Delta ADB\left(gg\right)\)
\(\Rightarrow\frac{AB}{AD}=\frac{AE}{AB}\Rightarrow AB^2=AD.AE\)
c) Vì OA là p/g \(\widehat{BOC}\Rightarrow\widehat{BOA}=\widehat{COA}=\frac{\widehat{BOC}}{2}\)
Do ABOC là tg nt\(\Rightarrow\widehat{BOA}=\widehat{BCA}\)(cùng chắn cung AB)
Suy ra \(\widehat{AOC}=\widehat{ACB}\)
Cho tứ giác ABCD nội tiếp đường tròn (O) có AB = BD. Các đường thẳng AB và DC cắt nhau tại N, đường thẳng CB cắt tiếp tuyến tại A của đường tròn (O) tại M. Chứng minh \(\widehat{AMN}=\widehat{ABD}\)
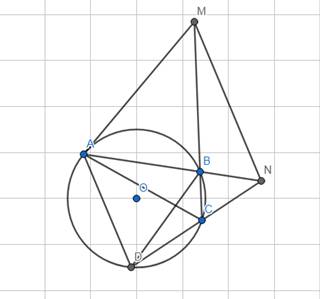
*Chứng minh AMNC là tứ giác nội tiếp.
Ta có AB=BD nên △ABD cân tại B.
\(\Rightarrow\widehat{ADB}=\widehat{BAD}\left(1\right)\)
Trong (O) có: \(\widehat{MAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AB.
\(\widehat{ADB}\) là góc nội tiếp chắn cung AB.
\(\Rightarrow\widehat{MAB}=\widehat{ADB}\left(2\right)\)
Tứ giác ABCD nội tiếp có \(\widehat{BCN}\) là góc ngoài ở đỉnh C.
\(\Rightarrow\widehat{BCN}=\widehat{BAD}\left(3\right)\)
(1), (2), (3) \(\Rightarrow\widehat{MAB}=\widehat{BCN}\).
\(\Rightarrow\)AMNC nội tiếp.
*Chứng minh yêu cầu đề bài.
AMNC nội tiếp \(\Rightarrow\widehat{AMN}=\widehat{ACD}\) (\(\widehat{ACD}\) là góc ngoài ở đỉnh C).
Mà \(\widehat{ACD}=\widehat{ABD}\) (ABCD nội tiếp)
\(\Rightarrow\widehat{AMN}=\widehat{ABD}\) (đpcm)
Cho tam giác ABC vuông ở A. Trên AC lấy một điểm M và vẽ đường tròn đường kính MC. Kẻ BM cắt đường tròn tại D. Đường thẳng DA cắt đường tròn tại S. Chứng minh rằng:
a) ABCD là một tứ giác nội tiếp;
b) \(\widehat{ABD}=\widehat{ACD};\)
c) CA là tia phân giác của góc SCB.
a, ta có ^BAC=900(góc nội tiếp chắn nửa đường tròn đường kính BC)
^MDC=900(góc nội tiếp chắn nửa đường tròn đường kính MC)
=>^BAC=^MDC(=900)
=>tứ giác ABCD nội tiếp (hai đỉnh A và D kề nhau cùng nhìn cạnh BC dưới hai góc bằng nhau)
b. vì tứ giác ABCD nội tiếp (câu a) nên ^ABD=^ACD (hai góc nội tiếp cùng chắn cung AD)
c, ta có bốn điểm D,S,C,M cùng thuộc đường tròn đường kính MC
=>tứ giác DSCM nội tiếp
=>^ADM=^SCM (cùng bù với ^MDS)
Mà ADCB nội tiếp nên ^ADM=^MCB( hai góc nội tiếp cùng chắn cung AB)
Do đó ^SCM=^MCB
=>CA là tia phân giác ^SCB
a) Ta có:\(\widehat{BAC}=90^o\) ⇒ A ∈ đường tròn đường kính BC.
D ∈ đường tròn đường kính MC
⇒ D ∈ đường tròn đường kính BC
⇒ A, B, C, D cùng thuộc đường tròn đường kính BC
hay tứ giác ABCD nội tiếp.
b) Xét đường tròn đường kính BC:
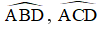
c) + Trong đường tròn đường kính MC:
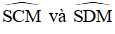
+ Trong đường tròn đường kính BD:
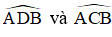
Cho hình thang cân ABCD (BC//AD), hai đường chéo AC, BD cắt nhau tại điểm O sao cho \widehat{BOC} = 60 độ. Gọi M,N,P,Q lần lượt là trung điểm của các đoạn thẳng BC,OA,AB,CD.a) Chứng minh tứ giác DMNC nội tiếp đượcb) Chứng minh tam giác MNQ là tam giác đềuc) So sánh các góc \widehat{MQP}, \widehat{QND}, \widehat{NMC} d) Chứng minh trực tâm của tam giác MNQ thẳng hàng với O, I
Cho hình thang cân ABCD (BC//AD), hai đường chéo AC, BD cắt nhau tại điểm O sao cho \widehat{BOC} = 60 độ. Gọi M,N,P,Q lần lượt là trung điểm của các đoạn thẳng BC,OA,AB,CD.a) Chứng minh tứ giác DMNC nội tiếp đượcb) Chứng minh tam giác MNQ là tam giác đềuc) So sánh các góc \widehat{MQP}, \widehat{QND}, \widehat{NMC} d) Chứng minh trực tâm của tam giác MNQ thẳng hàng với O, I
Cho tam giác ABC nội tiếp (O), H là trực tâm, AH cắt (O) tại E. Kẻ đường kính AOF. Chứng minh:
a) Tứ giác BCEF là hình thang cân
b) \(\widehat{BAE}=\widehat{CAF}\)
c) Gọi I là trung điểm của BC. Chứng minh: H, I, F thẳng hàng
a) Ta có B,C,F,E cùng thuộc đường tròn (O) => tứ giác BCEF nội tiếp
BCEF là hình thang cân
b) Ta có góc BAE = 90 độ - góc ABC = 90 độ - góc AFC = góc CAF
Suy ra: góc BAE = góc CAF
c) Ta có BH⊥AC
CF⊥AC
Suy ra BH//CF(1)
CH//BF(2)
Từ (1),(2)⇒tứ giác BHCF là hình bình hành
Mà I là trung điểm của BC
Suy ra I là trung điểm của HF hay I,H,F thẳng hàng