Question

Trong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Cho biết \(\widehat {ABC}\) = 70^o, \(\widehat {OCD}\) = 50o. Tìm góc \(\widehat {AOD}\).

Answer 1

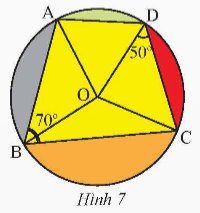
Tứ giác ABCD là tứ giác nội tiếp.

Do đó \(\widehat {ABC} + \widehat {ADC} = {180^o}\) suy ra \(\widehat {ADC} = {180^o} - \widehat {ABC} = {180^o} - {70^o} = {110^o}\).

Mà \(\widehat {ADO} + \widehat {OCD} = \widehat {ADC}\) suy ra \(\widehat {ADO} = {110^o} - {50^o} = {60^o}\).

Vì OA = OD = R nên tam giác OAD cân tại O

 Suy ra \(\widehat {OAD} = \widehat {ADO} = {60^o}\) (tính chất tam giác cân)

Vậy tam giác OAD đều suy ra \(\widehat {AOD} = {60^o}\).