Question

Cho tứ giác ABCD nội tiếp đường tròn (O) có AB = BD. Các đường thẳng AB và DC cắt nhau tại N, đường thẳng CB cắt tiếp tuyến tại A của đường tròn (O) tại M. Chứng minh \(\widehat{AMN}=\widehat{ABD}\)

Answer 1

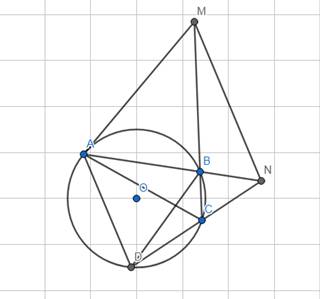
*Chứng minh AMNC là tứ giác nội tiếp.

Ta có AB=BD nên △ABD cân tại B.

\(\Rightarrow\widehat{ADB}=\widehat{BAD}\left(1\right)\)

Trong (O) có: \(\widehat{MAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AB.

\(\widehat{ADB}\) là góc nội tiếp chắn cung AB.

\(\Rightarrow\widehat{MAB}=\widehat{ADB}\left(2\right)\)

Tứ giác ABCD nội tiếp có \(\widehat{BCN}\) là góc ngoài ở đỉnh C.

\(\Rightarrow\widehat{BCN}=\widehat{BAD}\left(3\right)\)

(1), (2), (3) \(\Rightarrow\widehat{MAB}=\widehat{BCN}\).

\(\Rightarrow\)AMNC nội tiếp.

*Chứng minh yêu cầu đề bài.

AMNC nội tiếp \(\Rightarrow\widehat{AMN}=\widehat{ACD}\) (\(\widehat{ACD}\) là góc ngoài ở đỉnh C).

Mà \(\widehat{ACD}=\widehat{ABD}\) (ABCD nội tiếp)

\(\Rightarrow\widehat{AMN}=\widehat{ABD}\) (đpcm)