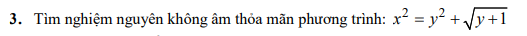Lời giải:
Ta xét 2 TH sau:
TH1: \(x\) lẻ:
PT \(\Leftrightarrow y^3=x^2-16=(x-4)(x+4)\)
Gọi \(d=(x-4,x+4)\Rightarrow \left\{\begin{matrix} x-4\vdots d\\ x+4\vdots d\end{matrix}\right.\Rightarrow 8\vdots d\)
Vì $x$ lẻ nên $x-4$ lẻ , do đó ước $d$ của nó cũng phải là số lẻ
\(\Rightarrow d=1\). Vậy $x-4,x+4$ nguyên tố cùng nhau
\(\Rightarrow x-4,x+4\) là hai số lập phương
Đặt \(x+4=u^3; x-4=v^3\) ( \(u>v\) nguyên lẻ)
\(\Rightarrow 8=u^3-v^3\)
\(\Leftrightarrow 8=(u-v)(u^2+uv+v^2)\)
Vì $u,v$ lẻ \(\rightarrow u^2+uv+v^2\) lẻ. Do đó \(u-v=8; u^2+uv+v^2=1\)
\(\Rightarrow (v+8)^2+v(v+8)+v^2=1\)
\(\Leftrightarrow 3v^2+24v+63=0\)
\(\Leftrightarrow v^2+8v+21=0\Leftrightarrow (v+4)^2+5=0\) (vô lý- loại)
TH2: $x$ chẵn \(\rightarrow y\) chẵn
\(\Rightarrow y^3\vdots 8\Rightarrow x^2=y^3+16\vdots 8\)
\(\Rightarrow x\vdots 4\) \(\Rightarrow x^2\vdots 16\Rightarrow y^3=x^2-16\vdots 16\Rightarrow y\vdots 4\)
Đặt \(x=4m, y=4n\). Rút gọn ta thu được pt:
\(m^2=4n^3+1\) \(\rightarrow m\) lẻ. Đặt \(m=2a+1(a\in\mathbb{Z})\) thì pt trở thành:
\((2a+1)^2=4n^3+1\)
\(\Leftrightarrow a^2+a=n^3\)
\(\Leftrightarrow n^3=a(a+1)\). Mà $(a,a+1)=1$ nên để tích của chúng là một số lập phương thì $a,a+1$ cũng là các số lập phương.
Đặt \(a=s^3; a+1=q^3(s< q)\)
\(\Rightarrow 1=q^3-s^3=(q-s)(q^2+qs+s^2)\)
\(\Rightarrow q-s=1=q^2+qs+s^2\)
\(\Rightarrow (q,s)=(0,-1); (1,0)\)
\(\Rightarrow (x,y)=(\pm 4,0)\)