Trong các dãy số sau, dãy số nào bị chặn?
A. Dãy \(\left(a_n\right)\), với \(a_n=\sqrt{n^3+n},\forall n\in N^*\).
B. Dãy \(\left(b_n\right)\), với \(b_n=n^2+\dfrac{1}{2n},\forall n\in N^*\).
C. Dãy \(\left(c_n\right)\), với \(c_n=\left(-2\right)^n+3,\forall n\in N^*\).
D. Dãy \(\left(d_n\right)\), với \(d_n=\dfrac{3n}{n^3+2},\forall n\in N^*\).
Nếu được thì giải thích chi tiết từng đáp án giúp mình với ạ, mình cảm ơn!















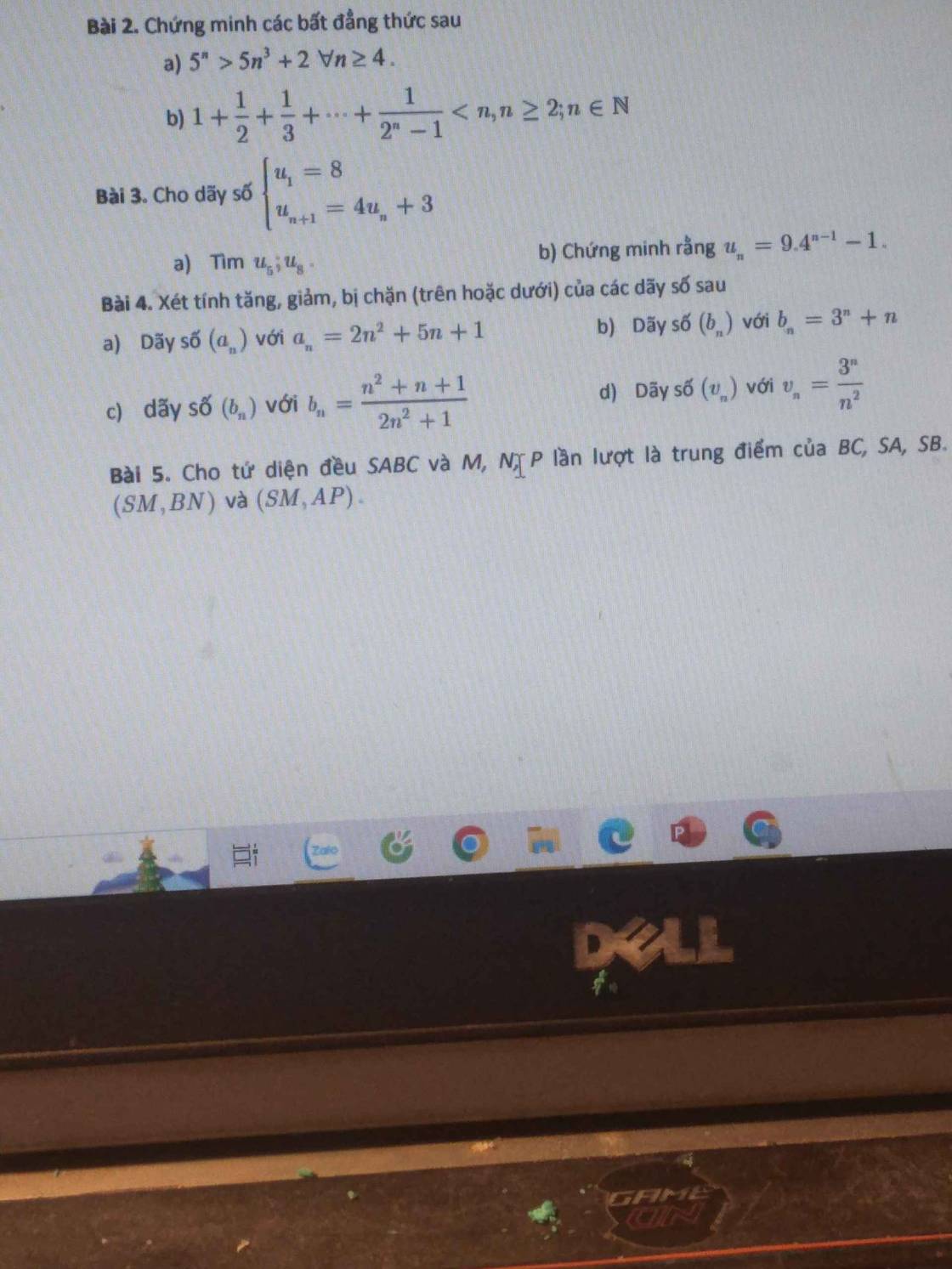 giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ
giúp em xét đãy số bị chặn của bài 4 với ạ. cần gấp ạ. Em cảm ơn ạ
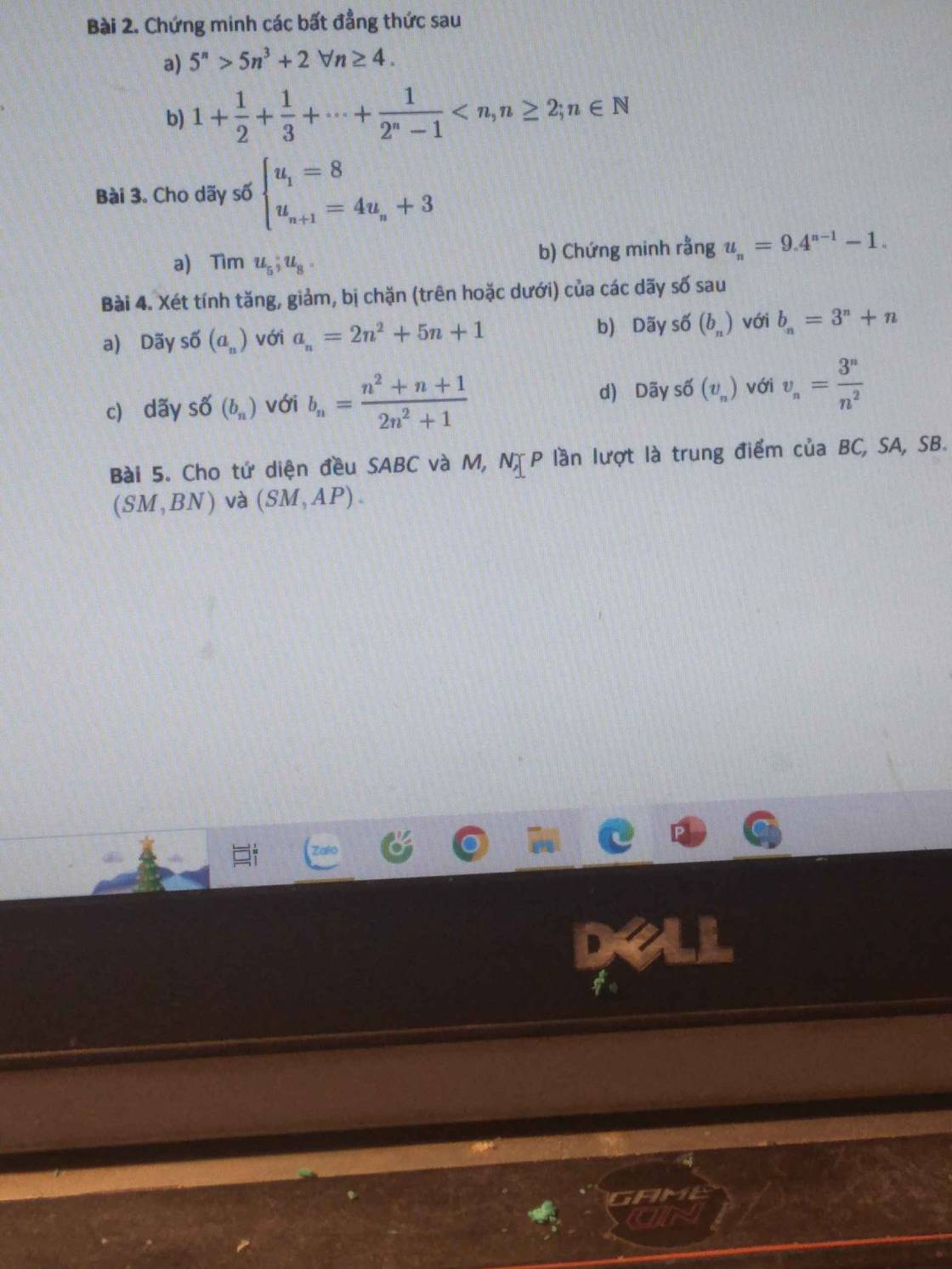 giúp em bài 4 với ạ. Pls
giúp em bài 4 với ạ. Pls