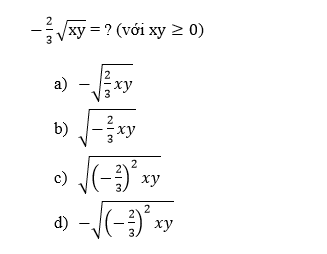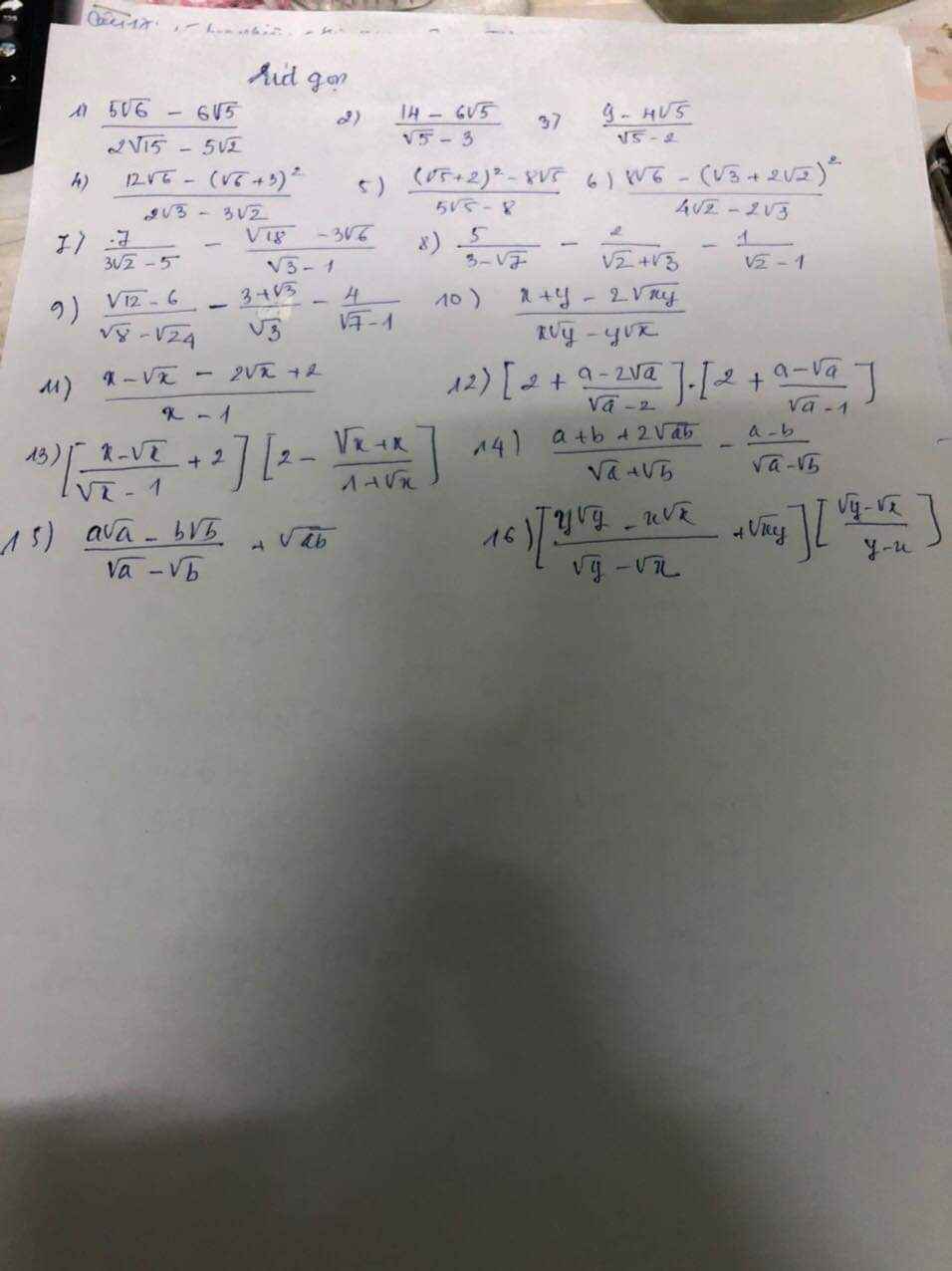\(căn 2008 trên x-4 =?\)
Bài 6: Biến đối đơn giản biểu thức chứa căn bậc hai
\(x+2y+2\sqrt{xy}-10\sqrt{x}-16\sqrt{y}+34=0\)
giải phương trình: \(\sqrt{3x^2-12x-6}\) +\(\sqrt{y^2-4y+13}\) =5
ai giải giúp bài 4 giúp mik i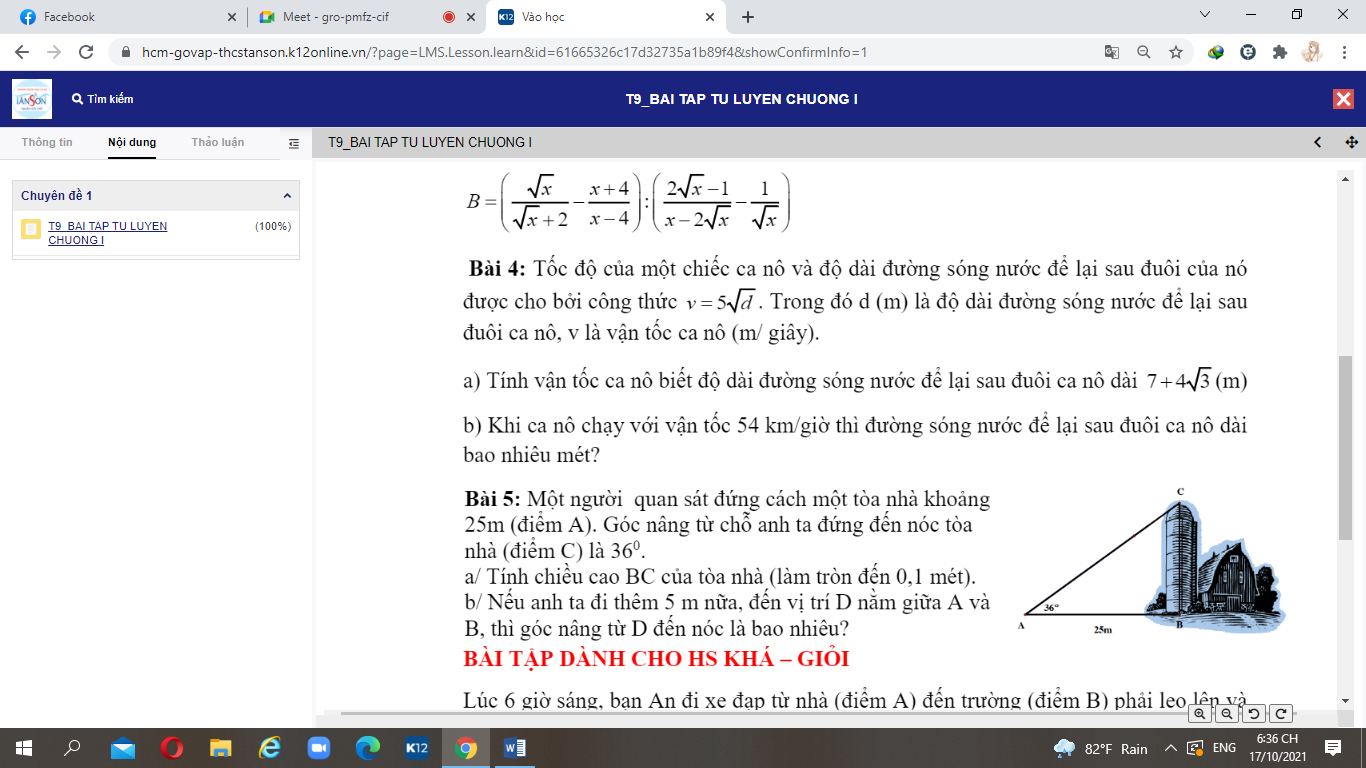
1/Đưa thừa số ra ngoài dấu căn: 3 căn8 - 5 căn 18 2/Đưa thừa số vào dấu căn So sánh: 7 căn3 và căn 141 3/ khử mẫu của biểu thức (bằng 2 cách) Căn 5 phần27 Căn 11 phần 64
Bài 1:a)sqrt{left(2sqrt{6}-4right)^2}+sqrt{15-6sqrt{6}}b) sqrt{left(3-2sqrt{2}right)^2}+sqrt{19+2sqrt{18}}c) sqrt{9+4sqrt{5}}-sqrt{left(1-sqrt{5}^2right)}Bài 2: Biến đổi biểu thứca) dfrac{1}{sqrt{7}+3}+dfrac{1}{sqrt{7}-3}b) dfrac{3}{sqrt{2}-1}+dfrac{sqrt{6}+sqrt{2}}{sqrt{3}+1}c) dfrac{1}{7+4sqrt{3}}+dfrac{1}{7-4sqrt{3}}
Đọc tiếp
Bài 1:
a)\(\sqrt{\left(2\sqrt{6}-4\right)^2}+\sqrt{15-6\sqrt{6}}\)
b) \(\sqrt{\left(3-2\sqrt{2}\right)^2}+\sqrt{19+2\sqrt{18}}\)
c) \(\sqrt{9+4\sqrt{5}}-\sqrt{\left(1-\sqrt{5}^2\right)}\)
Bài 2: Biến đổi biểu thức
a) \(\dfrac{1}{\sqrt{7}+3}+\dfrac{1}{\sqrt{7}-3}\)
b) \(\dfrac{3}{\sqrt{2}-1}+\dfrac{\sqrt{6}+\sqrt{2}}{\sqrt{3}+1}\)
c) \(\dfrac{1}{7+4\sqrt{3}}+\dfrac{1}{7-4\sqrt{3}}\)

giúp em tính góc C và các câu còn lại ạ
Tìm x thuộc R để M= \(\dfrac{1}{\sqrt{x}+1}-\dfrac{1-\sqrt{x}}{\sqrt{x+1}}\)có g.trị nguyên
mọi người giúp em với ạ ..................