Bài 6: Tính chất ba đường phân giác của tam giác

Gọi giao điểm của BG với AC là E,CG với AB là F

=>E là trung điểm của AC và F là trung điểm của AB

Xét ΔABE và ΔACF có

AB=AC

góc BAE chung

AE=AF

Do đo: ΔABE=ΔACF

Suy ra: BE=CF

mà BG=2/3BE

và CG=2/3CF

nên GB=GC

=>G nằm trên đường trung trực của BC(1)

Xét ΔIBC có \(\widehat{IBC}=\widehat{ICB}\)

nên ΔIBC cân tại I

=>IB=IC

=>I nằm trên đường trung trực của BC(2)

Ta có: AB=AC
nen A nằm trên đường trung trực của BC(3)

Từ (1), (2) và (3) suy ra A,G,I thẳng hàng

\(\widehat{ABC}+\widehat{ACB}=180^0-\widehat{BAC}\)

=>\(\widehat{IBC}+\widehat{ICB}=90^0-\dfrac{1}{2}\widehat{BAC}\)

\(\widehat{BIC}=180^0-\left(90^0-\dfrac{1}{2}\cdot\widehat{BAC}\right)=\dfrac{1}{2}\widehat{BAC}+90^0\)

Xét ΔADI vuông tại D và ΔAEI vuông tại E có

AI chung

\(\widehat{DAI}=\widehat{EAI}\)

Do đo: ΔADI=ΔAEI

Suy ra: AD=AE

hay ΔADE cân tại A

=>\(\widehat{ADE}=\dfrac{180^0-\widehat{A}}{2}\)

\(\widehat{BIC}+\widehat{ADE}=\dfrac{1}{2}\cdot\widehat{BAC}+90^0-\dfrac{1}{2}\cdot\widehat{BAC}+90^0=180^0\)

Gọi giao điểm của tia p/g của \(\widehat{B}\) và \(\widehat{C}\) với AC, AB lần lượt là K, H

Theo tính chất 3 đường phân giác của tam giác

=> AI là tia phân giác của \(\widehat{BAC}\)

Theo đề bài ta có: AB // DE

=> \(\widehat{HAI}=\widehat{AID}\) mà \(\widehat{HAI}=\widehat{DAI}\) => \(\widehat{AID}=\widehat{DAI}\)

=> tam giác DAI cân tại D

=> DA = DI

Cmtt ta có: tam giác IBE cân tại E

=> IE = EB

Ta có: DI + IE = DE

=> AD + EB = DE (đpcm)

Tick mình nha

a: Xét ΔPBC và ΔQCB có

PB=QC

góc PBC=góc QCB

BC chung

Do đó: ΔPBC=ΔQCB

Suy ra: \(\widehat{OBC}=\widehat{OCB}\)

hay ΔOBC cân tại O

b: Kẻ OH vuông góc với AB,OK vuông góc với AC

Xét ΔOHB vuông tại H và ΔOKC vuông tại K có

OB=OC

\(\widehat{OBH}=\widehat{OCK}\)

Do đó: ΔOHB=ΔOKC

Suy ra: OH=OK

c: Ta có: AB=AC

OB=OC

Do đó:AO là đường trung trực của BC

=>AO vuông góc với BC tại trung điểm của BC

Vì I cách đều ba cạnh nên BI và CI lần lượt là phân giác của góc ABC và ACB

=>\(\widehat{IBC}=\widehat{ICB}\)

=>ΔIBC cân tại I

=>IB=IC

=>I nằm trên đường trung trực của BC(1)

Gọi giao điểm của BG với AC là E, CG với AB là D

=>E là trung điểm của AC và D là trung điểm của AB

Xét ΔDBC và ΔECB có

DB=EC

góc DBC=góc ECB

BC chung

Do đó: ΔDBC=ΔECB

Suy ra: \(\widehat{GBC}=\widehat{GCB}\)

=>ΔGBC cân tạiG

=>G nằm trên đường trung trực của BC(2)

Ta có: AB=AC
nên A nằm trên đường trung trực của BC(3)

từ (1), (2)và (3) suy ra A,G,I thẳng hàng

Bài 2:

Xét ΔABC có

AI là phân giác

BI là phân giác

Do đó: I là tâm đường tròn nội tiếp ΔABC

=>CI là phân giác của góc ACB

Xét ΔMIB có \(\widehat{MIB}=\widehat{MBI}\)

nên ΔMIB cân tại M

Xét ΔNIC có \(\widehat{NIC}=\widehat{NCI}\)

nên ΔNIC cân tại N

MN=MI+IN

nên MN=MB+NC

Xét tam giác ABC với AH là đường trung tuyến đồng thời là đường trung trực nên :

AH ⊥ BC và HB = HC

Xét hai tam giác vuông HAB và HAC có:

HB = HC

= 90⁰

AH: cạnh chung

Nên ∆HAB = ∆HAC => AB = AC

Vậy ∆ABC cân tại A

bt2:

Đường tròn đi qua ba dỉnh của tam giác gọi là đường tròn ngoại tiếp tam giác đó. Đẻ vẽ đường tròn ngoại tiếp ta cần xác định tâm của đường tròn đó. Muốn xác định tâm ta vẽ hai đường trung trực và giao điểm hai đường trung trực ( cũng là giao điểm của ba trung trực cần tìm)

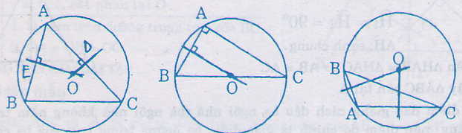
Nhận xét:

- Nếu tam giác có ba góc đều nhọn thì tâm đường tròn ngoại tiếp nằm trong tam giác.

- Nếu tam giác có góc vuông thì tâm đường tròn nằm trên cạnh huyền ( tâm là trung điểm của cạnh huyền)

- Nếu tam giác có góc tù thì tâm đường tròn ngoại tiếp nằm ngoài tam giác