Bài 1: Góc ở tâm. Số đo cung
Cho đường tròn (O), bán kính OA. Dây BC vuông góc với bán kính OA tại trung điểm H của OA. Tính số đo cung nhỏ BC và số đo cung lớn BC
Cho đường tròn (O; R). Vẽ dây AB sao cho số đo của cung nhỏ AB bằng \(\dfrac{1}{2}\) số đo cung lớn AB.
a) Tính góc ở tâm B
b) Tính độ dài dây AB theo R
Lời giải:
a. Câu hỏi chưa rõ ràng
b. Vì số đo cung nhỏ AB bằng một nửa số đo cung lớn AB mà tổng số
đo 2 cung bằng $360^0$ nên số đo cung nhỏ $AB$ là $120^0$
Từ $O$ kẻ $OH\perp AB$ như hình. Tam giác $OAB$ cân tại $O$ nên đường cao $OH$ đồng thời là đường phân giác, trung tuyến.
Do đó: $\widehat{AOH}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}.120^0=60^0$
$\frac{AH}{AO}=\sin \widehat{AOH}=\sin 60^0=\frac{\sqrt{3}}{2}$
$\Rightarrow AH=\frac{\sqrt{3}}{2}AO=\frac{\sqrt{3}}{2}R$
$\Rightarrow AB=2AH=\sqrt{3}R$
Đúng 1
Bình luận (0)
Cho hai đường tròn đồng tâm (O; R) và (O' R') với R > R'. Tiếp tuyến của đường tròn (O' R') tại A cắt đường tròn (O; R) tại B và C. Tia OA cắt đường tròn (O; R) tại E. So sánh \(\stackrel\frown{EB}\) và \(\stackrel\frown{EC}\)
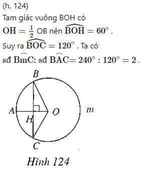
Cho tam giác cân AOB có \(\widehat{AOB}\) = 120°. Vẽ đường tròn (O; OA). Gọi M là một điểm nằm trên đường tròn, biết sđ\(\stackrel\frown{AM}\) = 50°. Tính số đo cung nhỏ BM và số đo cung lớn BM.
Cho hai đường tròn (O; R) và (O' R') cắt nhau tại A và B. Vẽ đường kính BOC và BO'D. So sánh số đo cung nhỏ AC và AD trong hai đường tròn đó, biết R > R'
Cho điểm A nằm ngoài đường tròn (O).Vẽ tiếp tuyến AB,AC và cát tuyến ADE.
a) chứng minh AB^2=AD.AE
b) Tia phân giác DBE cắt DE ở M.Chứng minh AB=AM và CM là tia phân giác của góc DCE
Trên hình bên, đồng hồ chỉ 14 giờ 29 phút 23 giây (14 : 29 : 23). Tính số đo cung của
a) Kim giờ và kim phút
b) Kim giờ và kim giây
c) Kim phút và kim giây
Khi đồng hồ chỉ 21 giờ 47 phút thì kim giờ và kim phút tạo thành một góc bao nhiêu độ?
Vì sao số đo cả đường tròn là 360° thay vì 100°?
100 độ là nó chưa được nửa đường tròn luôn á bạn
Đúng 0
Bình luận (0)