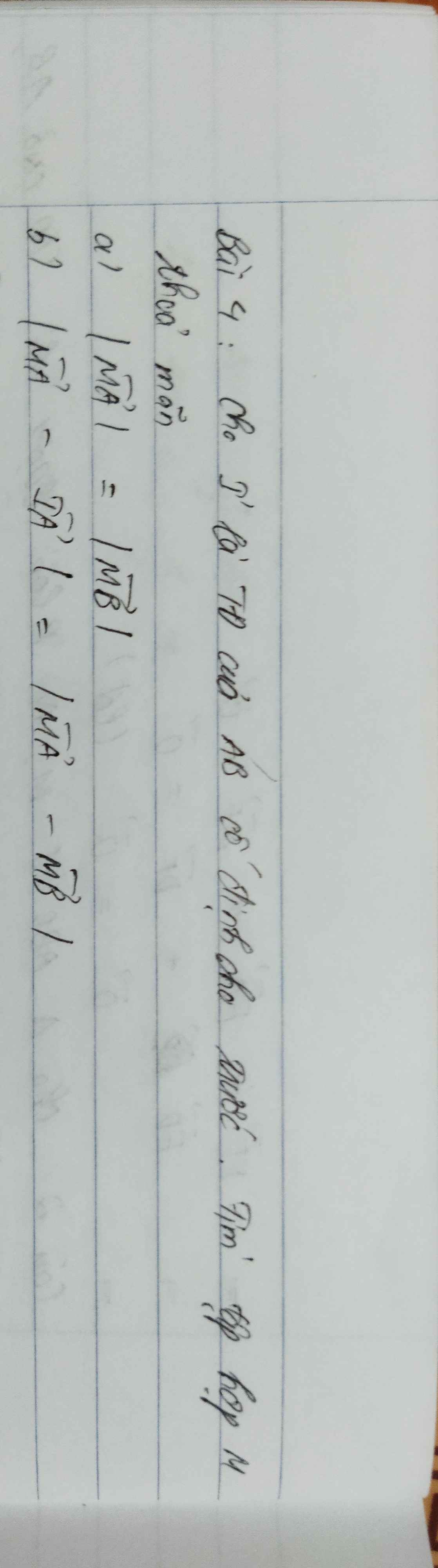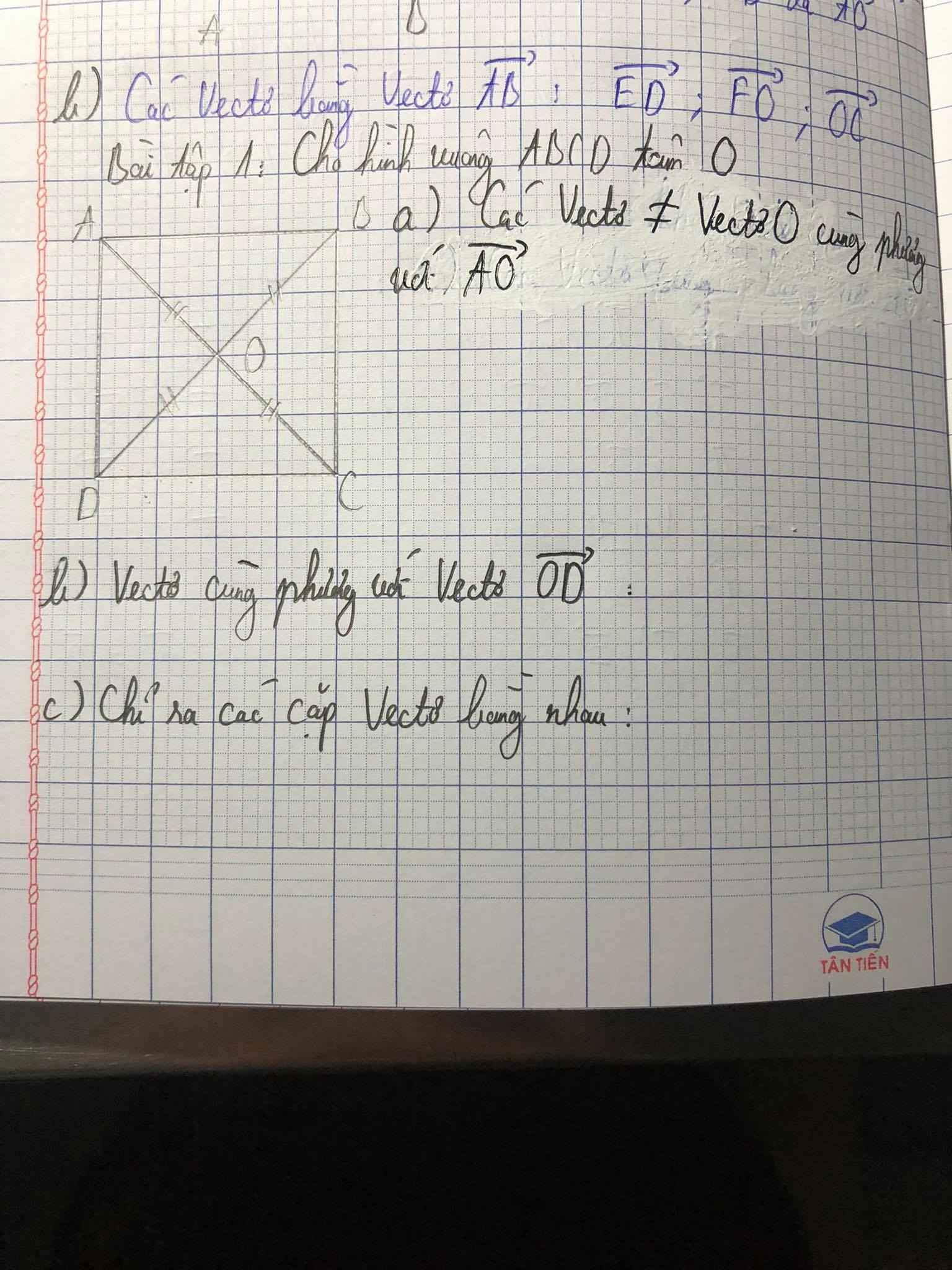Cho tam giác abc có trọng tâm g. Gọi M là trung điểm BC, lấy D đối xứng với G và M. Chứng minh VectoAG=vectoGD VectoBG=vectoDC
§1. Các định nghĩa
c: \(\overrightarrow{OA}=\overrightarrow{CO}\)
\(\overrightarrow{BO}=\overrightarrow{OD}\)
\(\overrightarrow{AB}=\overrightarrow{DC}\)
\(\overrightarrow{AD}=\overrightarrow{BC}\)
Đúng 0
Bình luận (1)
Giúp mình với ạ
12 tháng 7 2022 lúc 17:11
Chứng minh rằng tam giác ABC đều khi \(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\) = 0 với M , N , P là ba chân đường cao
a: vecto OC, vecto AC
b: vecto BO, vecto BD
c: vecto AO=vecto OC
vecto BO=vecto OD
vecto OA=vecto CO
vecto OB=vecto DO
vecto AB=vecto DC
vecto BA=vecto CA
vecto AD=vecto BC
vecto DA=vecto CB
Đúng 0
Bình luận (0)
Giúp mình câu này ạ. Cảm ơn ạ
a: I là trung điểm của BC
=>vecto BI=vecto IC
b: \(\overrightarrow{B'B}=\overrightarrow{AG}\)
=>\(2\cdot\overrightarrow{BJ}=2\cdot\overrightarrow{IG}\)
=>vecto BJ=vecto IG
Đúng 0
Bình luận (0)
Chứng minh rằng chỉ khi hai vectơ cùng phương, ta mới nói tới chúng cùng hướng hoặc ngược hướng
hai vecto cùng phương thì nò song song hoặc trùng nhau cái đã rồi mới tính tới cùng hướng hay ngược hướng
Đúng 0
Bình luận (0)
Mọi người giúp em với ạ !