a: vecto OC, vecto AC
b: vecto BO, vecto BD
c: vecto AO=vecto OC
vecto BO=vecto OD
vecto OA=vecto CO
vecto OB=vecto DO
vecto AB=vecto DC
vecto BA=vecto CA
vecto AD=vecto BC
vecto DA=vecto CB
cho 3 điểm A,B,C,D,E không thẳng hàng. liệt kê các vecto(khác vecto không) có điểm đâu là A hoặc B và điểm cuối bất kì
Cho tam giác ABC nội tiếp đường tròn tâm O, H là trực tâm của tam giác ABC, B' là điểm đối xứng với B qua O.
CM: \(\overrightarrow{AH}=\overrightarrow{B'C}\)
Cho đường tròn tâm 0 ,dây BC cố định , A là điểm dịch chuyển trên đường tròn, H là trực tâm tam giác ABC chứng minh khi A thay đổi thì véc tơ AH luôn bằng véc tơ cố định
Cho hình bình hành ABCD, tâm O. Hãy chỉ ra:
- các vectơ cùng hướng với vectơ OB
- các vectơ ngược hướng với vectơ OA
- các vectơ bằng nhau với vectơ OC
giúp mình nha, cảm ơn nhiều ^-^
Cho 2 hình bình hành ABCD và ABEF dựng vector EF và vector FQ sao cho bằng với vector AD. Chứng minh CDQP là hình bình hành.
cho ngũ giác ABCDE có bao nhiêu vecto khác 0 có điểm đầu cuối là đỉnh của ngũ giác đã cho?
Cho hình bình hành ABCD có tâm O. Gọi M, N lần lượt là trung điểm của AB, AD. Hãy tìm các vecto khác vecto không có điểm đầu và điểm cuối là các đỉnh của tứ giác: ngược hương với \(\overrightarrow{OB}\), bằng vecto \(\overrightarrow{OM}\).
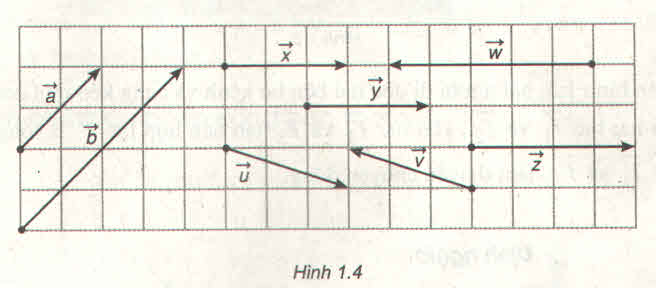
Trong hình 1.4 hãy chỉ ra các vectơ cùng phương, cùng hướng, ngược hướng và các vectơ bằng nhau :
Cho lục giác ABCDEF có tâm O
a) Tìm các vectơ khác \(\overrightarrow{0}\) và cùng phương với \(\overrightarrow{OA}\)
b) Tìm các vectơ bằng vectơ \(\overrightarrow{AB}\)
Xác định vị trí tương đối của ba điểm phân biệt A, B và C trong các trường hợp sau :
a) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng hướng, \(\left|\overrightarrow{AB}\right|>\left|\overrightarrow{AC}\right|\)
b) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) ngược hướng
c) \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) cùng phương
