Cho điểm M thỏa mãn \(\overrightarrow{OM}=2\overrightarrow{i}+\overrightarrow{j}\). Tọa độ của điểm M là:
A. M(0; 2; 1). B. M(1; 2; 0). C. M(2; 0; 1). D. M(2; 1; 0).
Bài tập cuối chương 2
Bài tập 1 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Thảo luận (1)
Bài tập 2 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Cho hai điểm A(−1; 2; −3) và B(2; −1; 0). Tọa độ của vectơ overrightarrow{AB} làA. overrightarrow{AB}left(1;-1;1right). B. overrightarrow{AB}left(3;3;-3right). C. overrightarrow{AB}left(1;1;-3right) D. overrightarrow{AB}left(3;-3;3right)
Đọc tiếp
Cho hai điểm A(−1; 2; −3) và B(2; −1; 0). Tọa độ của vectơ \(\overrightarrow{AB}\) là
A. \(\overrightarrow{AB}=\left(1;-1;1\right)\). B. \(\overrightarrow{AB}=\left(3;3;-3\right)\).
C. \(\overrightarrow{AB}=\left(1;1;-3\right)\) D. \(\overrightarrow{AB}=\left(3;-3;3\right)\)
Thảo luận (1)Hướng dẫn giảiChọn D
\(\overrightarrow {AB} = (2 - ( - 1); - 1 - 2;0 - ( - 3)) = (3; - 3;3)\)
(Trả lời bởi datcoder)
Bài tập 3 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Cho hai điểm A(3; −2; 3) và B(−1; 2; 5). Tọa độ trung điểm I của đoạn thẳng AB là
A. I(−2; 2; 1). B. I(1; 0; 4). C. I(2; 0; 8). D. I(2; −2; −1).
Thảo luận (1)Hướng dẫn giảiChọn B
\(M(\frac{{3 + ( - 1)}}{2};\frac{{ - 2 + 2}}{2};\frac{{3 + 5}}{2})\) hay M(1;0;4)
(Trả lời bởi datcoder)
Bài tập 4 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Cho ba điểm A(1; 3; 5), B(2; 0; 1), C(0; 9; 0). Tọa độ trọng tâm G của tam giác ABC là
A. G(3; 12; 6). B. G(1; 5; 2). C. G(1; 0; 5). D. G(1; 4; 2).
Thảo luận (1)Hướng dẫn giảiChọn D
\(G(\frac{{1 + 2 + 0}}{3};\frac{{3 + 0 + 9}}{3};\frac{{5 + 1 + 0}}{3})\) hay G(1;4;2)
(Trả lời bởi datcoder)
Bài tập 5 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Cho A(1; 2; −1), B(2; 1; −3), C(−3; 5; 1). Điểm D sao cho ABCD là hình bình hành có tọa độ là
A. D(−4; 6; 3). B. D(−2; 2; 5). C. D(−2; 8; −3). D. D(−4; 6; −5).
Thảo luận (1)Hướng dẫn giảiChọn A
Gọi \(D(x;y;z)\)
Ta có: \(\overrightarrow {AB} = (1; - 1; - 2)\); \(\overrightarrow {DC} = ( - 3 - x;5 - y;1 - z)\)
Để ABCD là hình bình hành thì \(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \left\{ \begin{array}{l}1 = - 3 - x\\ - 1 = 5 - y\\ - 2 = 1 - z\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 4\\y = 6\\z = 3\end{array} \right. \Rightarrow D( - 4;6;3)\)
(Trả lời bởi datcoder)
Bài tập 6 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Gọi α là góc giữa hai vectơ overrightarrow{u}left(0;-1;0right) và overrightarrow{v}left(sqrt{3};1;0right). Giá trị của α là:A. alphadfrac{pi}{6}. B. alphadfrac{pi}{3}. C. alphadfrac{2pi}{3}. D. alphadfrac{pi}{2}.
Đọc tiếp
Gọi α là góc giữa hai vectơ \(\overrightarrow{u}=\left(0;-1;0\right)\) và \(\overrightarrow{v}=\left(\sqrt{3};1;0\right)\). Giá trị của α là:
A. \(\alpha=\dfrac{\pi}{6}\). B. \(\alpha=\dfrac{\pi}{3}\). C. \(\alpha=\dfrac{2\pi}{3}\). D. \(\alpha=\dfrac{\pi}{2}\).
Thảo luận (1)Hướng dẫn giảiChọn C
\(\cos (\overrightarrow u ,\overrightarrow v ) = \frac{{\overrightarrow u .\overrightarrow v }}{{|\overrightarrow u |.|\overrightarrow v |}} = \frac{{0.\sqrt 3 - 1.1 + 0.0}}{{\sqrt {{1^2}} .\sqrt {{{(\sqrt 3 )}^2} + {1^2}} }} = - \frac{1}{2} \Rightarrow (\overrightarrow u ,\overrightarrow v ) = \frac{{2\pi }}{3}\)
(Trả lời bởi datcoder)
Bài tập 7 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Cho A(2; −1; 1), B(−1; 3; −1), C(5; −3; 4). Tích vô hướng \(\overrightarrow{AB}.\overrightarrow{BC}\) có giá trị là
A. 48. B. −48. C. 52. D. −52.
Thảo luận (1)Hướng dẫn giảiChọn D
Ta có: \(\overrightarrow {AB} = ( - 3;4; - 2)\); \(\overrightarrow {BC} = (6; - 6;5)\)
\(\overrightarrow {AB} .\overrightarrow {BC} = - 3.6 + 4.( - 6) - 2.5 = - 52\)
(Trả lời bởi datcoder)
Bài tập 8 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Cho hai điểm A(−1; 2; 3), B(1; 0; 2). Tọa độ điểm M thỏa mãn \(\overrightarrow{AB}=2\overrightarrow{MA}\) là
A. \(M\left(-2;3;\dfrac{7}{2}\right)\). B. \(M\left(-2;-3;\dfrac{7}{2}\right)\). C. M(-2; 3; 7). D. M(-4; 6; 7).
Thảo luận (1)Hướng dẫn giảiChọn A
Gọi \(M(x;y;z)\)
Ta có: \(\overrightarrow {AB} = (2; - 2; - 1)\), \(\overrightarrow {MA} = ( - 1 - x;2 - y;3 - z)\)
\(\overrightarrow {AB} = 2\overrightarrow {MA} \Leftrightarrow \left\{ \begin{array}{l}2 = 2( - 1 - x)\\ - 2 = 2(2 - y)\\ - 1 = 2(3 - z)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 3\\z = \frac{7}{2}\end{array} \right. \Rightarrow D( - 2;3;\frac{7}{2})\)
(Trả lời bởi datcoder)
Bài tập 9 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Trong không gian Oxyz, cho hình hộp chữ nhật OABC.O'A'B'C' như Hình 1, biết B'(2; 3; 5).
a) Tìm tọa độ các đỉnh còn lại của hình hộp.
b) Tính độ dài đường chéo OB' của hình hộp chữ nhật đó.
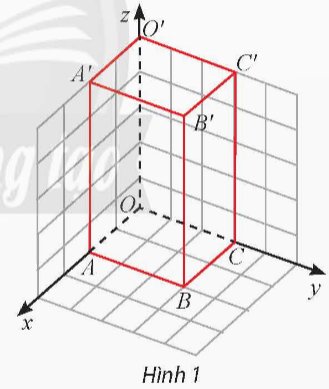
Thảo luận (1)Hướng dẫn giảia) O(0;0;0), A(2;0;0), B(2;3;0), C(0;3;0), O’(0;0;5), A’(2;0;5), C’(0;3;5)
b) \(\overrightarrow {OB'} = (2;3;5) \Rightarrow OB = \sqrt {{2^2} + {3^2} + {5^2}} = \sqrt {38} \)
(Trả lời bởi datcoder)
Bài tập 10 (SGK Chân trời sáng tạo - Tập 1 - Trang 65)
Tìm tọa độ của điểm P được biểu diễn trong Hình 2 và tính khoảng cách OP.
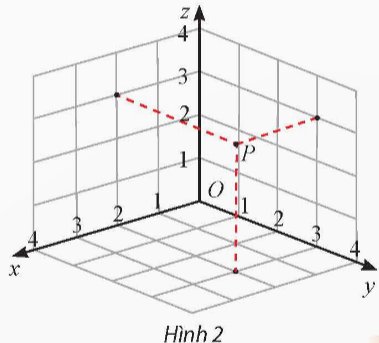
Thảo luận (1)Hướng dẫn giảiP(2;3;3) => \(\overrightarrow {OP} = (2;3;3) \Rightarrow OP = \sqrt {{2^2} + {3^2} + {3^2}} = \sqrt {22} \)
(Trả lời bởi datcoder)