Chương 1:ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ
Các câu hỏi tương tự
22 tháng 5 2022 lúc 15:36
Xét chiều biến thiên của hàm số \(y=\dfrac{1}{x+1}-2x\)
Xét sự biến thiên of hs y=
Bài 1: Xét tính đơn điệu của hàm số yf(x) khi biết đạo hàm của hàm số là:a) f(x)(x+1)(1-x^2)(2x-1)^3b) f(x)(x+2)(x-3)^2(x-4)^3Bài 2: Cho hàm số yf(x) có đạo hàm f(x)x(x+1)(x-2). Xét tính biến thiên của hàm số:a) yf(2-3x)b) yf(x^2+1)c) yf(3x+1)
Đọc tiếp
Bài 1: Xét tính đơn điệu của hàm số \(y=f(x)\) khi biết đạo hàm của hàm số là:
a) \(f'(x)=(x+1)(1-x^2)(2x-1)^3\)
b) \(f'(x)=(x+2)(x-3)^2(x-4)^3\)
Bài 2: Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=x(x+1)(x-2)\). Xét tính biến thiên của hàm số:
a) \(y=f(2-3x)\)
b) \(y=f(x^2+1)\)
c) \(y=f(3x+1)\)
cho hàm số y=(x-1)/(x+1) (C)
1,Khảo sát sự biến thiên và vẽ đồ thị hàm số
2,Tìm m để phương trình có nghiệm thuộc (0;π) : ((sinx-1)/(sinx+1))=m
Xét tính đồng biến, nghịch biến của hàm số và tìm cực trị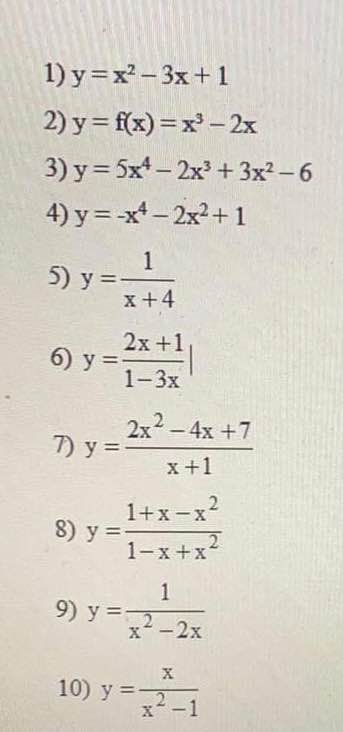
a) Khảo sát sự biến thiên và đồ thị (C) hàm số: f(x)=2x3+3x2+1
b) Tìm các giao điểm của đường cong (C) và parapol g(x) = 2x2+1 (P)
c) Viết Phương trình các tiếp điểm của (C) và (P) tại các điểm của chúng.
d) Xác định các khoảng trên đó (C) nằm phía trên và hoặc phía dưới (P).
Cho
hàm số y = (1)
1. Khảo sát sự biến thiên và vẽ đồ thị (C) với m = 1
2. Tìm m để hàm số (1) có 3 điểm cực trị là ba đỉnh của 1 tam giác vuông cân
7 tháng 8 2023 lúc 8:47
Câu 4. Cho hàm số \(y = x^4 - 2x^2 -3\). Mệnh đề nào sau đây là mệnh đề đúng?
A. Hàm số nghịch biến trên \((-1; 0).\)
B. Hàm số đồng biến trên \((-\infty;0).\)
C. Hàm số nghịch biến trên \((-1; 1).\)
D. Hàm số nghịch biến trên \((0; +\infty).\)
Xét tính đơn điệu của hàm số y= sinx trên \(\left(-\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\)