Nhìn đề đến một người theo Toán như anh còn thấy nản í :)
ừ thì năm nay lên 11 nma toi đ hiểu đây là cgi =))
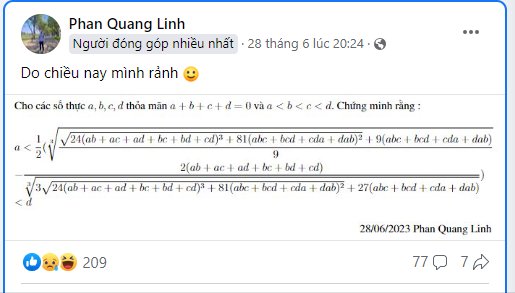
Cá nhân mình thấy không hay ho gì về việc bạn lấy đề người khác chế trên group Bất đẳng thức, thay đổi các biến rồi đem lên đây đánh đố mọi người. Điều này không thể hiện cái gì cả.
P/s: Nếu có đăng lại thì ít ra bạn cũng nên đăng đúng đề bài( Góp ý thẳng thắn cho bạn)