Giải:
Cách vẽ:
- Vẽ góc \(\widehat{xAy}\)=900
- Trên tia Ax vẽ đoạn thẳng AB= 3cm,
- Trên tia Ay vẽ đoạn thẳng AC= 3cm,
- Vẽ đoạn BC.
Ta vẽ được đoạn thẳng BC.
Ta đo các góc B và C ta được \(\widehat{B}=\widehat{C}\)=450
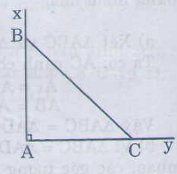
Giải:
Cách vẽ:
- Vẽ góc \(\widehat{xAy}\)=900
- Trên tia Ax vẽ đoạn thẳng AB= 3cm,
- Trên tia Ay vẽ đoạn thẳng AC= 3cm,
- Vẽ đoạn BC.
Ta vẽ được đoạn thẳng BC.
Ta đo các góc B và C ta được \(\widehat{B}=\widehat{C}\)=450
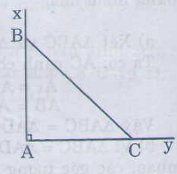
Vẽ tam giác ABC có \(\widehat{A}=90^0,AB=3cm,AC=1cm\). Sau đó đo góc C để kiểm tra rằng \(\widehat{C}=72^0\)
Vẽ tam giác ABC biết \(\widehat{B}=90^0,BA=BC=2,5cm\). Sau đó đo các góc A và C để kiểm tra rằng \(\widehat{A}=\widehat{C}=45^0\)
Cho tam giác ABC có \(\widehat{A}=110^0\), M là trung điểm của BC. Trên tia đối của tia MA lấy điểm K sao cho MK = MA
a) Tính số đo của góc ACK
b) Vẽ về phía ngoài của tam giác ABC các đoạn thẳng AD, AE sao cho AD vuông góc với AB và AD = AB, AE vuông góc với AC và AE = AC. Chứng minh rằng \(\Delta CAK=\Delta AED\)
c) Chứng minh rằng MA vuông góc với DE
Cho tam giác ABC có \(\widehat{A}=90^0\), trên cạnh BC lấy điểm E sao cho BE = BA. Tia phân giác của góc B cắt AC ở D
a) So sánh các độ dài DA và DE
b) Tính số đo góc BED
Trên hình 90 :
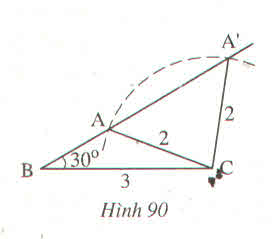
Các tam giác ABC và A'BC có cạnh chung BC = 3cm, CA = CA' = 2cm, \(\widehat{ABC}=\widehat{A'BC}=30^0\) nhưng hai tam giác đó không bằng nhau.
Tại sao ở đây không thể áp dụng trường hợp cạnh - góc - cạnh để kết luận \(\Delta ABC=\Delta A'BC\) ?
Cho tam giác ABC có \(\widehat{A}=90^0\). Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Trên tia đối của tia CB lấy điểm E sao cho CE = CB. Tính số đo của góc CDE ?
Cho tam giác ABC có 3 góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phỉa B đối với AC). Chứng minh rằng :
a) \(DC=BE\)
b) \(DC\perp BE\)
cho tam giác ABC Có Góc A > 90 độ. Về phía trong của tam giác vẽ Ax vuông góc với AB. Trên Ax lấy điểm D sao cho AD=AB. Kẻ Ay sao cho Ay vuông góc với AC, Trên Ay lấy điểm E sao cho AE=AC. M là trung điểm của DE. Trên tia đối của tia MA lấy F sao cho MF=MA
a, Chứng minh:góc yAB = góc xAC
b, Chứng minh: EF vuông góc với AB
c, Chứng minh:tam giác ABC=tam giác ABF