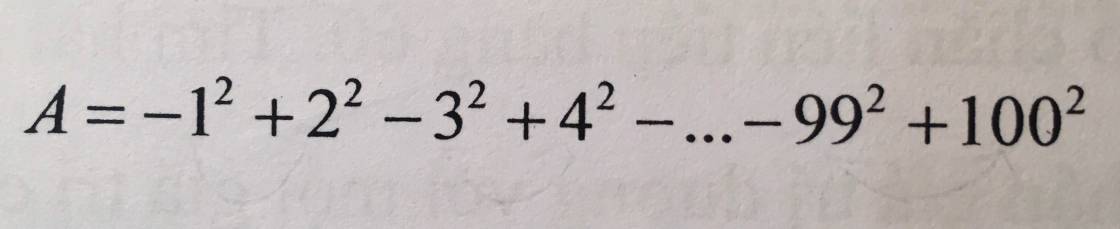Câu hỏi của Nhi Lê

Question

Tính nhanh: 1002-992+982-972+962-952+...22-12.

Phương Trâm · Accepted Answer

Đặt $A=100^2-99^2+98^2-97^2+96^2-95^2+...+2^2-1^2$

$A=\left(100^2-99^2\right)+\left(98^2-97^2\right)+...+\left(2^2-1^2\right)$

$A=2.100-1+2.98-1+2.96-1+...+2.2-1$

$A=2.\left(100+98+...+2\right)-50$

$A=\dfrac{2.\left[\left(100-2\right):2+1\right].\left(100+2\right)}{2}-50$

$A=50.102-50$

$A=50.\left(201-1\right)$

$A=50.101$

$A=5050$Câu trả lời: Đặt $A=100^2-99^2+98^2-97^2+96^2-95^2+...+2^2-1^2$