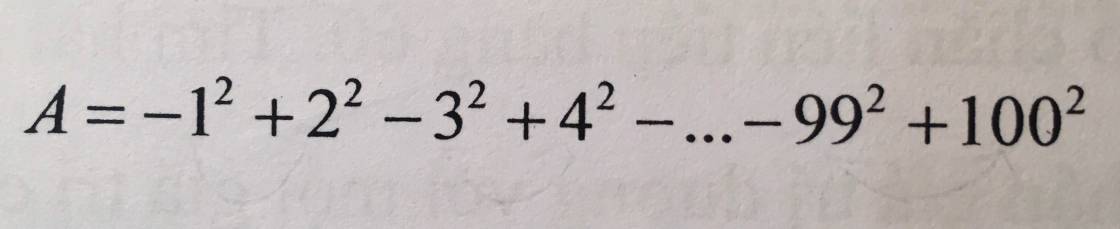Đặt A = \(100^2-99^2+98^2-97^2+96^2-95^2+2^2-1^2\)
A\(=\left(100-99\right)\left(100+99\right)+\left(98-97\right)\left(98+97\right)+\left(96-95\right)\left(96+95\right)+...+\left(2-1\right)\left(2+1\right)\)
A \(=199+195+191+...+3\)
A gồm \(\dfrac{\left(199-3\right)}{4}+1=50\) ( số hạng )
Vậy A = \(\dfrac{\left(199+3\right).50}{2}=5050\)
Thực hiện phép tính:
1002 - 992 + 982 - 972 +...+ 22 - 12
Bài 2: Tính nhanh.
1012, 10012, 1022, 992, 192, 9992
Tính nhanh :
978^2+22^2+978*44
Tính :
x^2+6x+9 với x=997
Tính nhanh
201822- 201722+ 201622-201522+...+222-1
So sánh
a)A=10002+10032+10052+10062 và B=10012+10022+10042+10072
( Làm hai cách )
Cho a=11...12
b=11...12
a có n số, b có n số
Chứng minh ab+1 là số chính phương
Nhanh nhaaaa
Tính giá trị biểu thức
A=x2 -2xy+y2 tại x=1002; y=2
B=y3 -9y2+27 tại y=1003
Giúp mình với ạ ! Mình cảm ơn nhìu :D Help me
Cần gấp ạ !
Tính nhanh:
Tính nhanh 199 mũ 2
Tính nhanh:
56.64
mik cần gấp ạ!
