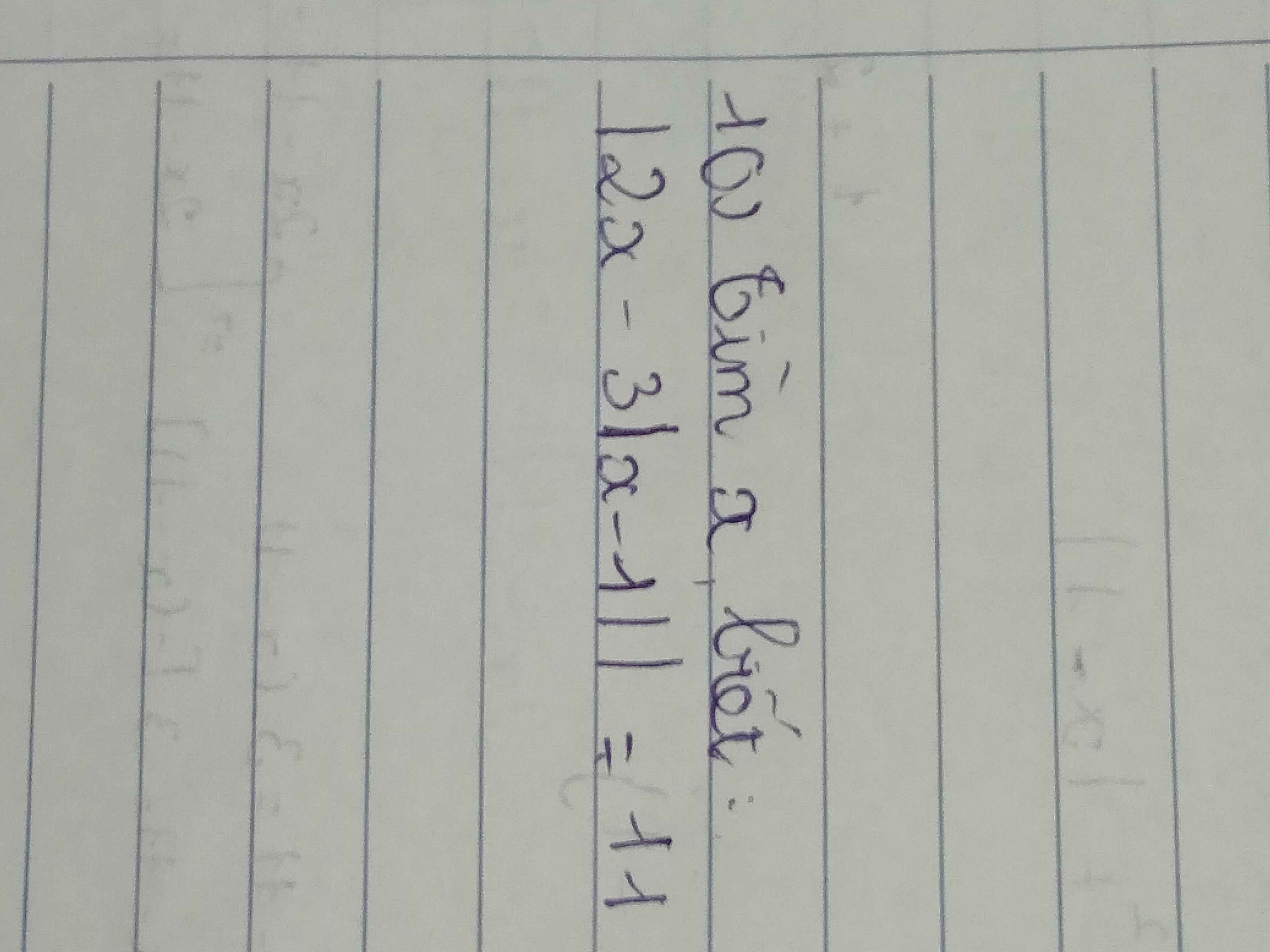Question

tìm x

/ 3 - 2x / - 3 = - (-3)

Answer 1

| 3 - 2x| -3 = -(-3)

=> |3 - 2x | = 3+3

=> |3-2x | = 6

=> \(\left[{}\begin{matrix}3-2x=6\\3-2x=-6\end{matrix}\right.\)

Sau đó tính ra từng trường hợp một nhé !

Answer 2

/ 3 - 2x / - 3 = - (-3)

/ 3 - 2x / -3 = 3

/ 3 - 2x / = 3 +3

/ 3 - 2x / = 6

Th1:

3- 2x = 6

2x = 3-6

2x = -3

x= (-3) :2

x= \(-\dfrac{3}{2}\)

Th2:

3 - 2x = -6

2x = 3 - (-6)

2x = 9

x = 9 : 2

x = \(\dfrac{9}{2}\)

Chúc bn hok tốt!

Answer 3

\(\left|3-2x\right|\) - 3 = -(-3)

⇒ \(\left|3-2x\right|\) = -(-3) + 3

⇒ \(\left|3-2x\right|\) = 9

⇒ 3 - 2x = 9 hoặc 3 - 2x = -9

Nếu 3 - 2x = 9 ⇒ 2x = -6 ⇒ x = -3

Nếu 3 -2x = -9 ⇒ 2x = 12 ⇒ x = 6

Vậy x = -3 hoặc x = 6

Answer 4

\(\left|3-2x\right|-3=-\left(-3\right)\)

\(\Leftrightarrow\left|3-2x\right|-3=3\)

\(\Leftrightarrow\left|3-2x\right|=3+3\)

\(\Leftrightarrow\left|3-2x\right|=6\)

\(\Leftrightarrow3-2x=\pm6\)

\(\Leftrightarrow\left[{}\begin{matrix}3-2x=6\\3-2x=-6\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=3-6\\2x=3-\left(-6\right)\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=-3\\2x=9\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=\dfrac{9}{2}\end{matrix}\right.\)

Vậy \(x=-\dfrac{3}{2}\) ; ​\(x=\dfrac{9}{2}\)​