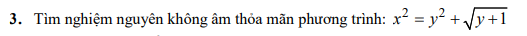Lời giải:
Ta có: \(3^x+16=5^y\)
Vì \(5^y>16\Rightarrow y>1\)
Khi đó: \(3^x=5^y-16\in\mathbb{Z}\Rightarrow x\geq 0\)
Vậy $x,y$ đều là các số nguyên không âm.
Xét hai TH sau:
TH1: $x$ lẻ: Đặt \(x=2k+1\)
\(\Rightarrow 3^x+16=3^{2k+1}+16=9^k.3+16\)
Thấy rằng:
\(9^k\equiv 1\pmod 8\Rightarrow 9^k.3+16\equiv 3+16\equiv 3\pmod 8\)
\(\Leftrightarrow 3^x+16\equiv 3\pmod 8\)
Lại có:
\(5^y=5^{2t}=25^t\equiv 1^t\equiv 1\not\equiv 3\pmod 8\) nếu $y$ chẵn
\(5^y=5^{2t+1}=25^t.5\equiv 1^t.5\equiv 5\not\equiv 3\pmod 8\) nếu $y$ lẻ
Do đó TH này vô lý
TH2: $x$ chẵn. Đặt \(x=2k\)
\(3^{x}+16=3^{2k}+16=9^k+16\equiv 1^k+16\equiv 1\pmod 8\)
Theo kết quả của TH1 thì \(5^y\equiv 1\pmod 8\) với $y$ chẵn và \(5^y\equiv 5\pmod 8\) với $y$ lẻ
Do đó để \(3^x+16=5^y\Rightarrow y\) chẵn. Đặt \(y=2t\)
Khi đó: \(3^{2k}+16=5^{2t}\)
\(\Leftrightarrow 16=(5^t-3^k)(5^t+3^k)\)
Thấy \(5^t-3^k, 5^t+3^k\) có cùng tính chẵn lẻ, \(5^t+3^k>5^t-3^k,5^t+3^k>0\) nên ta chỉ thu được TH duy nhất là:
\(\left\{\begin{matrix} 5^t+3^k=8\\ 5^t-3^k=2\end{matrix}\right.\) \(\Rightarrow 2.5^t=10\Leftrightarrow t=1\rightarrow k=1\)
Do đó \(x=y=2\)
Thử lại thấy thỏa mãn. Vậy \(x=y=2\)