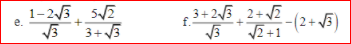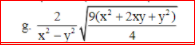b , Ta có : \(\dfrac{x\sqrt{x}-y\sqrt{y}}{\sqrt{x}-\sqrt{y}}=\dfrac{\left(\sqrt{x}\right)^3-\left(\sqrt{y}\right)^3}{\left(\sqrt{x}-\sqrt{y}\right)}\) = \(\dfrac{\left(\sqrt{x}-\sqrt{y}\right)\left(x+\sqrt{xy}+y\right)}{\sqrt{x}-\sqrt{y}}=x+\sqrt{xy}+y\)
d , Ta có : \(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{1-a}\right)^2=\left(\dfrac{1-a\sqrt{a}+\sqrt{a}-a}{1-\sqrt{a}}\right)\dfrac{\left(1-\sqrt{a}\right)^2}{\left(1-a\right)^2}\)= \(\dfrac{\left(1-a\right)+\sqrt{a}\left(1-a\right)}{1-\sqrt{a}}.\dfrac{\left(1-\sqrt{a}\right)^2}{\left(1-a\right)^2}\)
= \(\dfrac{\left(1-a\right)\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)^2}{\left(1-\sqrt{a}\right)\left(1-a\right)^2}\)
= \(\dfrac{\left(1+\sqrt{a}\right)\left(1-\sqrt{a}\right)}{\left(1-a\right)}=\dfrac{\left(1-a\right)}{\left(1-a\right)}=1\)
\(2\sqrt{3a}-\sqrt{75a}+\sqrt{\dfrac{13,5}{2a}}-\dfrac{2}{5}\sqrt{300a^3}\left(a>0\right)\)
=\(2\sqrt{3a}-\sqrt{5^2\cdot3a}+a\sqrt{\dfrac{13,5\cdot2a}{\left(2a\right)^2}}-\dfrac{2}{5}\sqrt{10^2\cdot a^2\cdot2}\)
=\(\left(2-5+\dfrac{3}{2}-4a\right)\sqrt{a}\)
=\(\dfrac{-11}{2}a\sqrt{a}\)