Độ dài cung tròn \(l\) chính bằng chu vi của đáy nón
\(\Rightarrow l=2\pi r=6\pi\)
Khi khai triển ta được đường tròn có bán kính \(R=5\)
\(\Rightarrow\) Số đo cung: \(n=\frac{180l}{\pi R}=\frac{180.6\pi}{\pi.5}=216^0\)
Một hình nón có bán kính đường tròn đáy là 3cm, đường sinh là 5cm. Cắt hình nón đó theo một đường sinh và trải ra trên một mặt phẳng ta được một hình quạt tròn. Số đo của cung tròn hình quạt tròn đó là:
A. 1260
B. 1500
C. 2160
D. 2500
Nón lá dùng để che nắng, mưa, làm quạt khi nóng. Ngày nay nón lá cũng được xem là món quà đặc biệt cho du khách khi đến thăm quan Việt Nam. Biết một chiếc nón lá dạng hình nón cls đường sinh bằng 35cm, đường kính vành nón bằng 50cm. Người ta dùng hai lớp lá để phủ lên bề mặt xung quanh của nón. Tính diện tích lá cần dùng cho một chiếc nón đó (lấy \(\pi\approx3,14\))
Cho hình thang cân ABCD (AD//CB) có AB = 12cm, AC = 16cm, BC = 20cm
C/m: A, B, C, D thuộc một đường tròn, tính bán kính của đường tròn đó
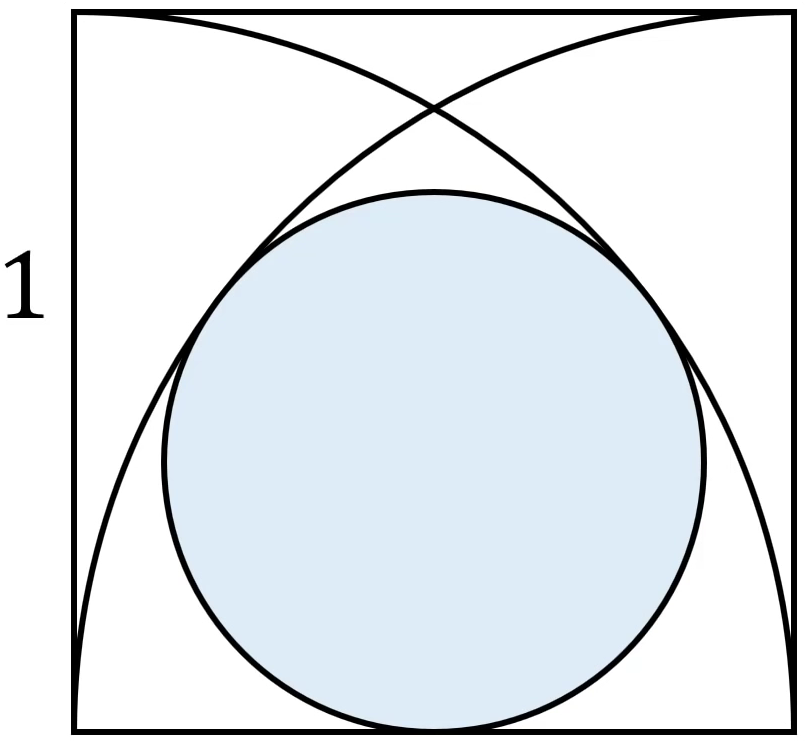
Cho hình vuông có cạnh bằng 1 cm. Trên đó dựng hai nửa đường tròn có đường kính là cạnh của hình vuông như hình vẽ. Hãy tính bạn kính hình tròn màu xanh.
Trong vườn trường, người ta xây một bồn hoa gồm hai hình tròn tâm A và tâm B tiếp xúc ngoài với nhau có AB=3m. Tính bán kính của mỗi hình tròn biết diện tích bồn hoa bằng \(4,68\pi m^2\) và bán kính của hình tròn tâm A lớn hơn bán kính của hình tròn tâm B
Cho tam giác ABC nội tiếp trong đường tròn tâm 0.M là một điểm bất kỳ trên đường tròn đó. Gọi A, B',C' lần lượt là hình chiếu của M trên các đường thắng BC, CA, AB.
a) Chứng minh các tứ giác BC AM và CA MB nội tiếp.
b) Chứng minh 3 diểm A' , B', C' thẳng hàng.
c) Trên đường tròn tâm O dã cho lấy điểm \(M_1\ne M\). Gọi lần lượt là hình chiếu của \(M_1\) lên các đường thằng BC, CA, AB. Tim vị trí của điểm M, trên dường tròn tâm O để đường thẳng \(A_1B_1\) , vuông góc với đường thẳng B'C'.
Cho đường tròn tâm O bán kính R và đường thẳng(Δ)không có điểm chung với đường tròn tâm( O), H là hình chiếu vuông góc của O trên (Δ) .từ điểm M bất kì trên (Δ) ( M không trùng H), vẽ 2 tiếp tuyến MA, MB với đường tròn (O) (A,B là hai tiếp điểm ).Gọi I, K theo thứ tự là giao điểm của AB với OM và OH
1. Chứng minh AB = 2 .AK với 5 điểmM ,A ,O, B, H cùng thuộc đường tròn
2 .Chứng minh OI.OH = OK.OM = \(R^2\)
3.trên đoạn OA lấy điểm N sao cho AN = 2ON. đường trung trực của BN cắt OM ở E .tính tỉ số\(\dfrac{OE}{OM}\)
a, CM : góc COD = 90o
b, CM : CD = AC + BD
c, gọi H là hình chiếu của M trên AB , I là giao điểm BC và MH . CM : IM = IH
Cho đường tròn (O;R), điểm A ở ngoài đường tròn có OA=2R. Từ A kẻ hai tiếp tuyến AB, AC (B, C là hai tiếp điểm)
a. Chứng minh OA ⊥ BC
b. OA cắt đường tròn (O) tại D. Chứng minh tứ giác BOCD là hình thoi
c. Tính AB và diện tích tam giác ABC theo R
d. Chứng minh D là tâm đường tròn nội tiếp tam giác ABC và tính bán kính của của đường tròn đó theo R
