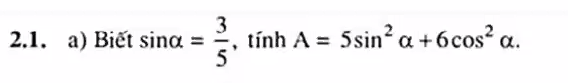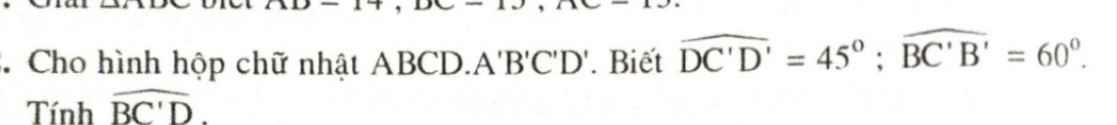Dạng 2:
a) \(\left(1-\cos\alpha\right)\left(1+\cos\alpha\right)=1-\cos^2\alpha=\sin^2\alpha\)
b) \(\sin\alpha-\sin\alpha\cdot\cos^2\alpha=\sin\alpha\left(1-\cos^2\alpha\right)=\sin^3\alpha\)
c) Ta có: \(\sin^4\alpha+\cos^4\alpha+2\cdot\sin^2\alpha\cdot\cos^2\alpha\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^2\)
\(=1^2=1\)
d) Ta có: \(\tan^2\alpha-\sin^2\alpha\cdot\tan^2\alpha\)
\(=\tan^2\alpha\left(1-\sin^2\alpha\right)\)
\(=\tan^2\alpha\cdot\cos^2\alpha\)
\(=\dfrac{\sin^2\alpha}{\cos^2\alpha}\cdot\cos^2\alpha=\sin^2\alpha\)

 mong mn giúp em, em cần gấp
mong mn giúp em, em cần gấp