Bài 6: Tam giác cân
Các câu hỏi tương tự
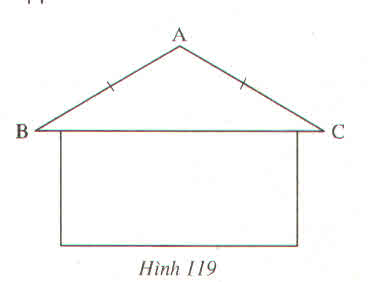
Hai thanh AB và AC của vì kèo một mái nhà bằng nhau ( h.119 ) và thường tạo với nhau một góc hing : a ) 145 nếu mái là tôn , b ) 100 ° nếu mái là ngói . Tính góc ABC trong từng trường hợp .
Xem chi tiết
Cho tam giác ABC cân tại A, Â = 120° Từ B kẻ đường thẳng vuông góc với AB, từ C kẻ đường thẳng vuông góc với AC, hai đường thẳng này cắt nhau tại D. a) Chứng minh ∆DAB = ∆DAC b) Chứng minh ∆ DBC là tam giác đều. c) Gọi H là giao điểm của AD và BC . Chứng minh 2BH + AD > AB + BD.
Cho ABC là tam giác đều, biết D là trung điểm của BC, góc D vuông, AD vuông góc với BC, E là trung điểm của cạnh AC. Chứng minh rằng:
a) Tam giác ABD = tam giác AMC và BD=CD
b) Tính AD nếu BC = 6cm
c) Tam giác EDC đều
d) DE//AB
Xem chi tiết
Cho tam giác abc cân tại a.Qua b kẻ đường thẳng vuông góc với ab,qua c kẻ đường thẳng vuông góc với ac,chúng cắt nhau tại d.Chứng minh rằng:câu a: tam giác abd bằng tam giác acd,câu b: ad là tia phân giác của bac
Xem chi tiết
Cho góc xOy có số đo \(120^0\), điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox (B thuộc Ox), kẻ AC vuông góc với Oy (C thuộc Oy). Tam giác ABC là tam giác gì ? Vì sao ?
Cho tam giác ABC có A bằng 90 độ qua đỉnh B có tam giác kẻ đường thẳng xy vuông góc với AB ( AC , By thuộc cùng thuộc cùng một nửa mặt phẳng có bờ là đường thẳng chứa cạnh AB )
a chứng minh xy song song với AC
b Biết CBy = 30 Tính các góc còn lại của tam giác ABC
Cho tam giác ABC vuông tại A có AB = 3cm, AC = 4cm.
a) Tính độ dài cạnh BC
b) Vẽ đường phân giác BD của tam giác ABC (D thuộc AC). Vẽ DE vuông góc BC tại E. Chứng minh tam giác ABD = tam giác EBD và Góc BED = 90 độ
c)Hai đường thẳng AB và ĐE cắt nhau tại F. Chứng minh BI là đường trung trực của EF
d) Gọi I là giao điểm của BD và FC. Chứng minh BI là đường trung trực của EF
Cho tam giác ABC cân tại A. Các tia phân giác của góc B và góc C cắt nhau tại O. Qua O kẻ đường thẳng song song với BC. Đường thẳng này cắt cạnh AB tại E và cắt cạnh AC tại F.
a) Tìm những tam giác cân có trên hình vẽ
b) Tìm những cặp tam giác cân bằng nhau
Cho tam giác ABC cân ở A. Qua B vẽ đường thẳng vuông góc với AB , qua C vẽ đường thẳng vuông góc với AC, hai đường thẳng này cắt nhau ở D. Chứng minh:
a) BD = CD
b) AD là đường trung trực của BC