Giúp mình vs! Nhất là hai câu cuối !!
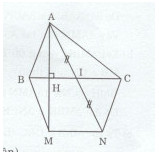
Cho tam giác ABC nhọn (AB < AC) . Kẻ AH vuông góc BC tại H . Trên tia đối của tia HA lấy điểm M sao cho H là trung điểm của AM
a/ Chứng minh : △ABH=△MBH
b/ Chứng minh : Góc BAC = Góc BMC
c/ Gọi I là trung điểm của BC . Trên tia đối của tia IA lấy điểm N sao cho I là trung điểm của AN . Chứng minh : NC = BM
d/ Cho AB = 13 cm , AH = 12 cm , HC = 16 cm .Tính độ dài cạnh AC , BC
c) Theo câu a) ta có \(\Delta ABH=\Delta MBH.\)
=> \(AB=BM\) (2 cạnh tương ứng).
Xét 2 \(\Delta\) \(ABI\) và \(NCI\) có:
\(AI=NI\) (vì I là trung điểm của \(AN\))
\(\widehat{AIB}=\widehat{NIC}\) (vì 2 góc đối đỉnh)
\(BI=CI\) (vì I là trung điểm của \(BC\))
=> \(\Delta ABI=\Delta NCI\left(c-g-c\right)\)
=> \(AB=NC\) (2 cạnh tương ứng).
Mà \(AB=BM\left(cmt\right)\)
=> \(NC=BM.\)
d) Xét \(\Delta ACH\) vuông tại \(H\left(gt\right)\) có:
\(AC^2=AH^2+HC^2\) (định lí Py - ta - go).
=> \(AC^2=12^2+16^2\)
=> \(AC^2=144+256\)
=> \(AC^2=400\)
=> \(AC=20\left(cm\right)\) (vì \(AC>0\)).
+ Xét \(\Delta ABH\) vuông tại \(H\left(gt\right)\) có:
\(AB^2=AH^2+BH^2\) (định lí Py - ta - go).
=> \(13^2=12^2+BH^2\)
=> \(BH^2=13^2-12^2\)
=> \(BH^2=169-144\)
=> \(BH^2=25\)
=> \(BH=5\left(cm\right)\) (vì \(BH>0\)).
+ Ta có: \(BC=BH+HC.\)
=> \(BC=5+16\)
=> \(BC=21\left(cm\right).\)
Vậy \(AC=20\left(cm\right);BC=21\left(cm\right).\)
Chúc bạn học tốt!













