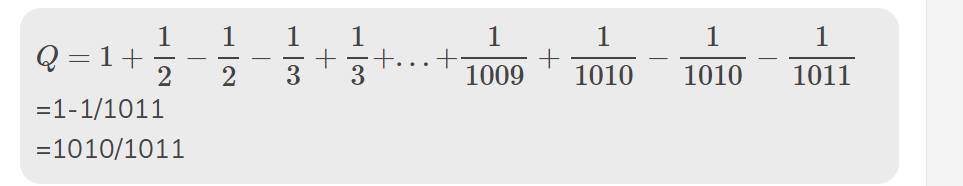Đại số lớp 7
Các câu hỏi tương tự
CMR:\(\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+\frac{7}{\left(3.4\right)^2}+...+\frac{19}{\left(9.10\right)^2}< 1\)
\(A=\frac{3}{\left(1.2\right)^2}+\frac{5}{\left(2.3\right)^2}+...+\frac{101}{\left(50.51\right)^2}\)
GIÚP MÌNH NHA CHIỀU MÌNH SẮP NỘP RÙI
Chứng minh: \(1.2+2.3+3.4+......+n\left(n+1\right)⋮3\)
chứng minh rằng:
\(\frac{1.2-1}{2!}+\frac{2.3-1}{3!}+\frac{3.4-1}{4!}+...+\frac{99.100-1}{100!}< 2\)
mình ngu toán chúng minh (hép mi)
tính Q
Q=\(\frac{1.98+2.97+3.96+...+2.97+1.98}{1.2+2.3+3.4+...+96.97+97.98+98.99}\)
S=\(\dfrac{5}{1.2}\)+\(\dfrac{13}{2.3}\)+\(\dfrac{25}{3.4}\)+\(\dfrac{41}{4.5}\)+...+\(\dfrac{181}{9.10}\)
22 tháng 11 2021 lúc 10:42
Tính A = 1.2 + 2.3 + 3.4 + … + n.(n + 1)
Tính A = [1 + (1 + 2) + (1 + 2 + 3) + ..... + (1 + 2 + 3 + ..... + 98)]/(1.2 + 2.3 + 3.4 + ..... + 98.99)
Tính
S=\(\frac{5}{1.2}\)+\(\frac{13}{2.3}\)+\(\frac{25}{3.4}\)+\(\frac{41}{4.5}\)+....+\(\frac{181}{9.10}\)
Tính A = 1.2 + 2.3 + 3.4 + … + n.(n + 1)