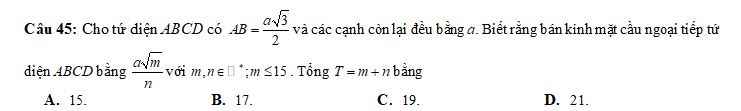Giúp mình câu hỏi này với ạ.
Đề bài: Khi sản xuất vỏ lon sữa Ông Thọ hình trụ, nhà sản xuất luôn đặt tiêu chí sao cho chi phí sản xuất vỏ lon là nhỏ nhất, tức nguyên liệu được dùng là ít nhất. Hỏi khi đó tổng diện tích toàn phần của lon sữa là bao nhiêu khi nhà sản xuất muốn thể tích của hộp là \(Vcm^3\).
Các đáp án lựa chọn là:
\(A.S_{tp}=6\sqrt[3]{\dfrac{\pi V^2}{4}}\) \(B.S_{tp}=3\sqrt[]{\dfrac{\pi V^2}{4}}\) \(C.S_{tp}=3\sqrt[3]{\dfrac{\pi V^2}{4}}\) \(D.S_{tp}=6\sqrt[]{\dfrac{\pi V^2}{4}}\)
Gọi chiều cao của lon sữa là \(h\), bán kính đáy là R
Ta có \(V=\pi R^2h\Rightarrow h=\dfrac{V}{\pi R^2}\)
Lon sữa sẽ tốn ít nguyên liệu nhất khi diện tích toàn phần của lon sữa là nhỏ nhất
\(S_{tp}=2\pi R^2+2\pi Rh=2\pi R^2+2\pi R.\dfrac{V}{\pi R^2}=2\pi R^2+\dfrac{2V}{R}\)
Xét hàm \(f\left(R\right)=2\pi R^2+\dfrac{2V}{R}\Rightarrow f'\left(R\right)=4\pi R-\dfrac{2V}{R^2}\)
\(f'\left(R\right)=0\Rightarrow4\pi R-\dfrac{2V}{R^2}=0\Rightarrow R^3=\dfrac{V}{2\pi}\Rightarrow R=\sqrt[3]{\dfrac{V}{2\pi}}\)
Dựa vào BBT ta thấy hàm \(f\left(R\right)\) đạt cực tiểu tại \(R=\sqrt[3]{\dfrac{V}{2\pi}}\)
Vậy diện tích toàn phần nhỏ nhất của lon sữa là:
\(S_{tp}=2\pi R^2+\dfrac{2V}{R}=2\pi\sqrt[3]{\dfrac{V^2}{4\pi^2}}+2V.\sqrt[3]{\dfrac{2\pi}{V}}=6\sqrt[3]{\dfrac{\pi V^2}{4}}\)
Đáp án A