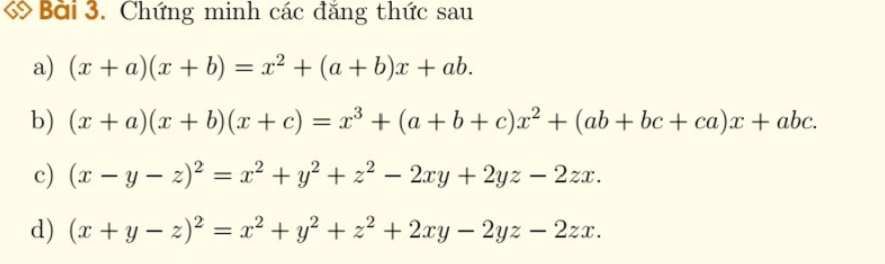`c, (x+a)(x+b)(x+c) = x^3 + (a+b+c)x^2 + (ab+bc+ca)x + abc`
Xét vế trái:
`(x+a)(x+b)(x+c)`
`= (x^2 + ax + bx + ab)(x + c)`
`= x^3 + ax^2 + bx^2 + abx + cx^2 + acx + bcx + abc`
`= x^3 + x^2(a+b+c) + x(ab+bc+ca) + abc = VP => dpcm`.
`c, (x-y-z)^2 = x^2 + y^2 +z^2 -2xy + 2yz - 2zx`.
Xét vế trái `= (x-y-z)^2`
`= (x-y-z)(x-y-z) = x^2 - xy - xz -xy + y^2 + yz -zx + yz + z^2`
`= x^2+y^2+z^2-2xy+2yz-2zx`