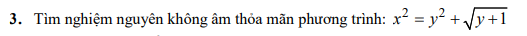Ta có \(x^2;y^2;z^2\equiv0;1;4\) (mod 8)
\(\Rightarrow x^2+y^2+z^2\equiv0;1;2;3;4;5;6\left(mod8\right)\).
Mà \(8t^2-1\equiv7\left(mod8\right)\)
Nên phương trình đã cho vô nghiệm.
Violympic toán 9
Các câu hỏi tương tự
1) Chứng minh rằng: \(x^3-7y=51\) không có nghiệm nguyên
2) Tìm nghiệm nguyên của phương trình \(x^2-5y^2=27\)
3) Tìm nghiệm nguyên dương
a) \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=1\)
b)\(\dfrac{1}{x}+\dfrac{1}{y}=z\)
Giải phương trình nghiệm nguyên \(x^2+y^2+2x+2y=x^2y^2-1\)
4 tháng 7 2021 lúc 8:49
Tìm nghiệm nguyên dương của phương trình : 2xyz=x+y+z
Giair Hệ phương trình nghiệm nguyên : \(\left\{{}\begin{matrix}x+y+z=3\\x^3+y^3+z^3=3\end{matrix}\right.\)
Tìm nghiệm nguyên dương của phương trình : \(\sqrt{x+2\sqrt{3}}=\sqrt{y}+\sqrt{z}\)
Giair Hệ phương trình nghiệm nguyên : \(\left\{{}\begin{matrix}5x+3y+\dfrac{z}{3}=100\\x+y+z=100\end{matrix}\right.\)
Cho hệ phương trình \(|^{mx+2y=1}_{3x+\left(m+1\right)y=-1}\) (với m là tham số)
a) Giải hệ phương trình với m = 3.
b) Giải và biện luận hệ phương trình theo m.
c) Tìm m để hệ phương trình có nghiệm là số nguyên.
Tìm nghiệm nguyên ko âm của phương trình: x²=y²+y+1
1. Tìm nghiệm nguyên của phương trình xy-x+y=4
Tìm nghiệm nguyên không âm thỏa mãn phương trình: x^2=y^2 + căn y+1