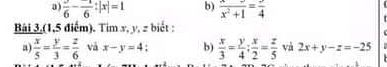Có \(P=\left(1+\dfrac{x}{y}\right)\left(1+\dfrac{y}{z}\right)\left(1+\dfrac{z}{x}\right)\\ =\dfrac{y+x}{y}\cdot\dfrac{z+y}{z}\cdot\dfrac{x+z}{x}\)
Áp dụng t/c của DTSBN , ta đc :
\(\dfrac{y+z-x}{x}=\dfrac{z+x-y}{y}=\dfrac{x+y-z}{z}\\ = \dfrac{y+z-x+z+x-y+x+y-z}{x+y+z}\\ =\dfrac{\left(y+y-y\right)+\left(x+x-x\right)+\left(z+z-z\right)}{x+y+z}\\ =\dfrac{x+y+z}{x+y+z}=1\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{y+z-x}{x}=1\\\dfrac{z+x-y}{y}=1\\\dfrac{x+y-z}{z}=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y+z-x=x\\z+x-y=y\\x+y-z=z\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}y+z=2x\\z+x=2y\\x+y=2z\end{matrix}\right.\left(1\right)\)
Thay `(1)` vào `P` ta có :
\(P=\dfrac{2z}{y}\cdot\dfrac{2x}{z}\cdot\dfrac{2y}{x}=\dfrac{8xyz}{xyz}=8\)










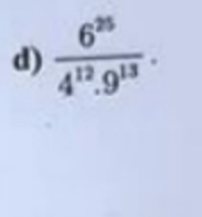 cần gấp
cần gấp