Lời giải:
Muốn biết điểm nào thuộc đường tròn, ta chỉ cần thay tọa độ $(x,y)$ tương ứng của điểm đó vào PT đường tròn, nếu thỏa mãn thì điểm đó thuộc đường tròn.
Thực hiện phép thay thử ta thấy đáp án D là đáp án đúng.
Lời giải:
Muốn biết điểm nào thuộc đường tròn, ta chỉ cần thay tọa độ $(x,y)$ tương ứng của điểm đó vào PT đường tròn, nếu thỏa mãn thì điểm đó thuộc đường tròn.
Thực hiện phép thay thử ta thấy đáp án D là đáp án đúng.
Phần I. Trắc nghiệm (2 điểm)
Câu 1: Điều kiện xác định của biểu thức 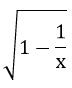
A.x ≠ 0 B.x ≥ 1 C.x ≥ 1 hoặc x < 0 D.0 < x ≤ 1
Câu 2: Đường thẳng 2x + 3y = 5 đi qua điểm nào trong các điểm sau đây
A. ( 1; -1) B. ( 2; -3) C. ( -1; 1) D. (- 2; 3)
Câu 3: Cho phương trình x – 2y = 2 (1). Phương trình nào trong các phương trình sau đây kết hợp với (1) để được phương trình vô số nghiệm
A.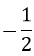
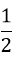
C.2x - 3y = 3 D.2x - 4y = -4
Câu 4: Tọa độ giao điểm của (P) y = 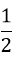
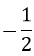
A. (2; 2) B. ( 2; 2) và (0; 0)
C.(-3; 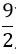
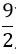
Câu 5: Giá trị của k để phương trình x2 + 3x + 2k = 0 có 2 nghiệm trái dấu là:
A. k > 0 B. k < 0 C. k > 2 D. k < 2
Câu 6: Cho tam giác ABC vuông tại A có AB : AC = 3 : 4 và đường cao AH bằng 9 cm. Khi đó độ dài đoạn thẳng HC bằng:
A. 12 cm B. 9 cm C. 6 cm D. 15 cm
Câu 7: Cho hai đường tròn (O; 3cm) và (O; 4cm) có OO' = 5 cm. Vị trí tương đối của 2 đường tròn là:
A. Hai đường tròn tiếp xúc ngoài với nhau
B. Hai đường tròn tiếp xúc trong với nhau
C. Hai đường tròn không giao nhau
D. Hai đường tròn cắt nhau
Câu 8: Thể tích hình cầu thay đổi như thế nào nếu bán kính hình cầu tăng gấp 2 lần
A. Tăng gấp 16 lần B. Tăng gấp 8 lần
C. Tăng gấp 4 lần D. Tăng gấp 2 lần
a) viết phương trình đường tròn (C) có tâm I(2,3) đi qua điểm A(5,7) b) viết phương trình tiếp tuyến của đường tròn (C) : (x-1)^2 + ( y+5)^2 =4 . Biết tiếp tuyến song song với đường thẳng (d) 3x + 4y - 1 =0
Cho d : \(\left\{{}\begin{matrix}x=2+3t\\y=5-4t\end{matrix}\right.\) . Điểm nào sau đây không thuộc d ?
A . A ( 5 ; 3 )
B . B ( 2 ; 5 )
C . C ( -1 ; 9 )
D . D ( 8 ; -3 )
Trình bày bài làm cụ thể rồi ms chọn đáp án nha các bạn .
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \(\left(x-1\right)^2+\left(y-2\right)^2=4\) và hai điểm \(A\left(1;4\right);B\left(1;\dfrac{1}{2}\right)\). Viết phương trình đường thẳng d đi qua B cắt đường tròn (C) tại M, N sao cho tam giác AMN có diện tích lớn nhất
Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) \(x^2+y^2-2x-4=0\) và đường thẳng (d): \(x-y+1=0\)
1) Viết pt đường thẳng (d1) vuông góc với (d) và tiếp xúc với (C)
2) Viết pt đương thẳng (Δ) song song với (d) và cắt (C) tại 2 điểm M, N có MN = 2
3) Tìm trên (d) điểm P biết rằng qua P kẻ được 2 tiếp tuyến PA, PB đến (C) có ΔPAB là tam giác đều. (trong đó A, B là 2 tiếp điểm)
. Cho điểm A(1; 2) và đường thẳng d: 2x - 3y - 1 = 0 Viết phương trình đường thẳng delta đi qua A và vuông góc với d.
Khoảng cách từ điểm M ( 0 ; 1 ) đến đường thẳng \(\Delta\) : \(5x-12y-1=0\) bằng :
A . \(\frac{11}{13}\)
B . \(\frac{13}{17}\)
C . 1
D . \(\sqrt{13}\)
Trình bày bài làm cụ thể rồi mới chọn đáp án nha các bạn .
Đường tròn \(x^2+y^2-2x-2y-23=0\) cắt đường thẳng \(x-y+2=0\) theo một dây cung có độ dài bằng bao nhiêu ?
A . 5
B . \(2\sqrt{23}\)
C . 10
D . \(5\sqrt{2}\)
Trình bày bài làm cụ thể rồi ms chọn đáp án nha các bạn .
Câu 3. Cho điểm A(1; 2) và đường thẳng d: 2x - 3y - 1 = 0 Viết phương trình đường thẳng triangle delta*i qua A và song song với d.