Xét ΔOAB và ΔODC có
\(\widehat{OAB}=\widehat{ODC}\)
\(\widehat{AOB}=\widehat{DOC}\)
Do đó: ΔOAB\(\sim\)ΔODC
SUy ra: OA/OD=OB/OC
hay \(OA\cdot OC=OB\cdot OD\)
Cho tứ giác lồi ABCD thỏa mãn \(\widehat{BAD}+\widehat{BCD}=180^0\). Gọi I là giao điểm của AC và BD. Gọi M là trung điểm của đoạn thẳng AB, và N là trung điểm của đoạn thẳng CD.
Chứng minh rằng \(\widehat{AIM}=\widehat{DIN}\) .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ cho em với ạ! Em cám ơn nhiều lắm ạ!
Cho hình thoi ABCD có \(\widehat{ABC}< 90^0\). Gọi O là giao điểm của 2 đường chéo AC và BD. Kẻ OH vuông góc với BC. Gọi M và N là 2 điểm lần lượt thuộc DC và DA, sao cho \(\widehat{MON}=\widehat{DAC}\). Chứng minh rằng 3 đường thẳng BM ; HN và AC đồng quy tại I
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán hỗ trợ giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều lắm ạ!
Cho tam giác ABC (AB < AC). Phân giác trong AD. Trên tia đối của tia DA lấy I sao cho \(\widehat{BAD}\) = \(\widehat{DCI}\)
a) Chứng minh \(\Delta ADB\sim\Delta DCI\)
b) Chứng minh \(\dfrac{AD}{AC}\)=\(\dfrac{AB}{AI}\)
c) Chứng minh AD2 = AB.AC - DB.DC
d) Gọi AE là phân giác ngoài của \(\Delta ABC\) (\(E\in BC\)). Chứng minh \(\dfrac{DB}{DC}\) = \(\dfrac{EB}{EC}\)và AE2 = EC.EB - AB.AC
Cho tam giác ABC vuông tại A có AB = 1cm, AC = 3cm. Trên cạnh AC lấy các điểm D, E sao cho AD = DE = EC.
a) Tính độ dài BD.
b) Chứng minh tam giác BDE đồng dạng với tam giác CDB.
c) Tính \(\widehat{DEB}+\widehat{DCB}\)
Cho tam giác ABC cân tại A có BC = 2a, M là trung điểm của BC. Lấy các điểm D, E theo thứ tự thuộc các cạch AB, AC sao cho \(\widehat{DME}\) = \(\widehat{B}\)
a) Chứng minh BC. CE không đổi.
b) Chứng minh DM là tia phân giác của góc BDE.
c) Tính chu vi tam giác AED nếu tam giác ABC đều.
Cho △ABC cân tại A, có \(\widehat{A}=20^o\), AB = AC = b, BC = a. Trên cạnh AC lấy điểm D sao cho \(\widehat{DBC}=20^o\).
a) Chứng minh : △BDC \(\sim\) △ABC
b) Vẽ AE ⊥ BD tại E. Tính độ dài các đoạn thẳng AD,DE,AE
c) Chứng minh \(a^3+b^3=3ab^2\)
Mik làm được câu (a) và câu (b) rồi ! Giúp mik câu (c) ạ :33
Cho tam giác ABC cân tại đỉnh A , có đường cao AH. Gọi M là 1 điểm di động trên cạnh BC. Điểm D và E lần lượt thuộc cạnh AB và AC sao cho tứ giác ADME là hình bình hành. Gọi I là giao điểm của BE và CD.
a) Chứng minh rằng : \(\widehat{DMI}=\widehat{AME}\)
b) Chứng minh rằng đường thẳng MI luôn luôn đi qua 1 điểm cố định .
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán giúp đỡ, em cám ơn nhiều lắm ạ!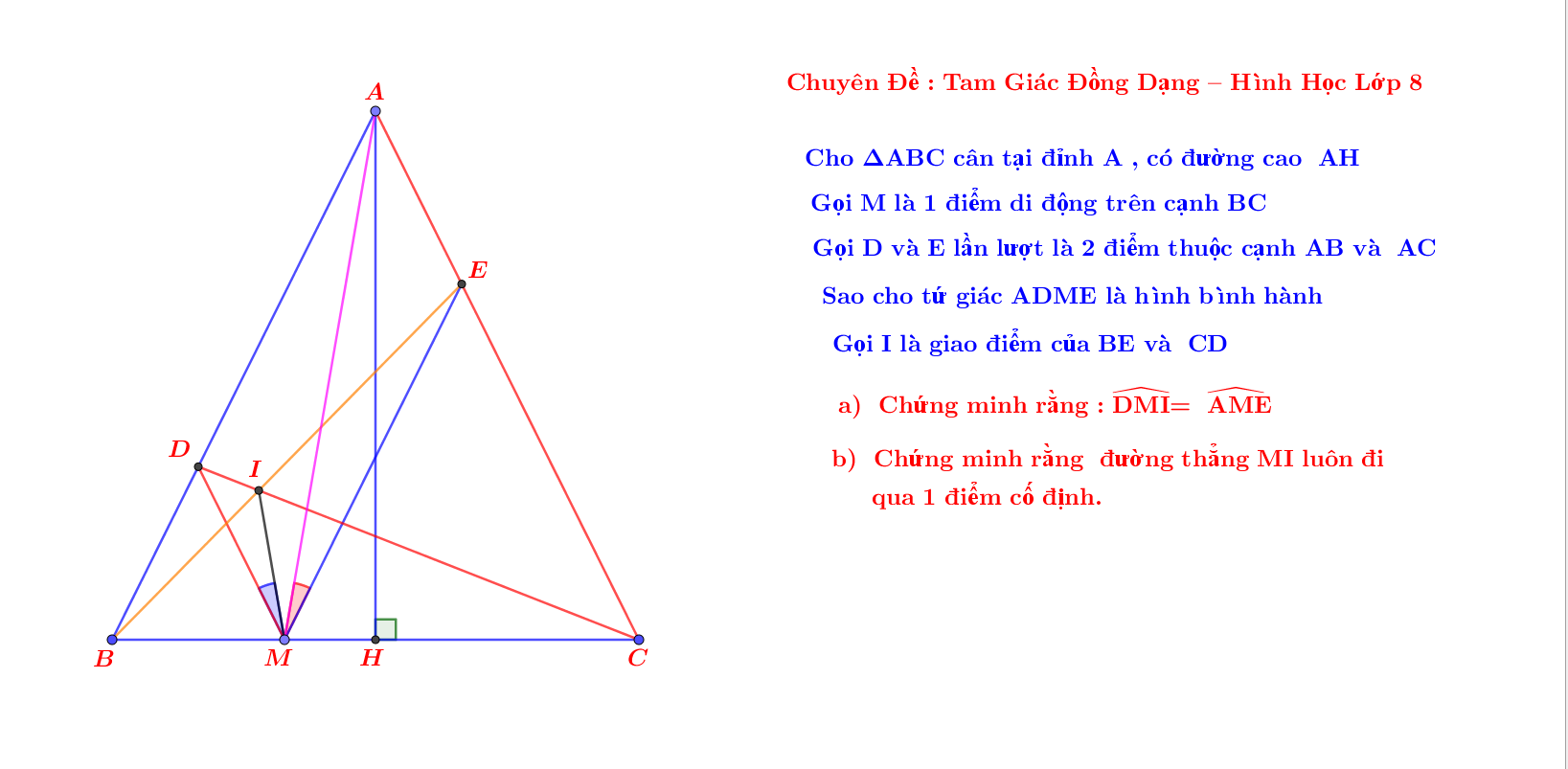
Bổ Toán Bổ Đề Về Tính Chất Đường Phân Giác Trong Tam Giác
'' Cho tam giác ABC cân tại đỉnh A. Gọi M là trung điểm của đoạn thẳng BC. Gọi D và E là hai điểm lần lượt thuộc AB và AC sao cho \(\widehat{DME}=\widehat{ABC}\)
a) Chứng minh rằng tam giác BMD đồng dạng với tam giác CEM.
b) Chứng minh rằng DM là tia phân giác của góc \(\widehat{BDE}\).
P/s: Em nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em tham khảo với ạ!
Em cám ơn nhiều ạ!
Bài 1. Cho tứ giác ABCD có E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Biết AC = BD và AC vuông góc BD. Chứng minh: a) EFGH là hình bình hành. b) EFGH là hình chữ nhật. c) EFGH là hình thoi. d) EFGH là hình vuông
